题目内容
若直线AB，BC的倾斜角分别为α，β，且α=β，则直线AB，BC的位置关系是 ．
考点：直线的倾斜角
专题：直线与圆
分析：由两直线倾斜角相等，知二直线平行，再由二直线有公共点，知二直线重合．
解答：
解：∵直线AB，BC的倾斜角分别为α，β，且α=β，
∴tanα=tanβ或tanα与tanβ同时不存在，
∴直线AB，BC平行或重合，
又直线AB与直线BC有一个公共点B，
∴直线AB、BC重合．
故答案为：重合．
∴tanα=tanβ或tanα与tanβ同时不存在，
∴直线AB，BC平行或重合，
又直线AB与直线BC有一个公共点B，
∴直线AB、BC重合．
故答案为：重合．
点评：本题考查两直线的位置关系的判断，是基础题，解题时要认真审题，注意直线与直线平行的性质的合理运用．
练习册系列答案
相关题目
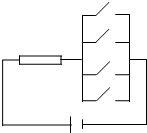某种开关在电路中闭合的概率为p，现将4只这种开关并联在某电路中（如图所示），若该电路为通路的概率为| 65 |
| 81 |
A、
| ||
B、
| ||
C、
| ||
D、
|
与函数y=x为相同函数的是（ ）
A、y=
| ||
B、y=
| ||
| C、y=elnx | ||
| D、y=log22x |
已知点（3，1）和（-4，6）在直线3x-2y+m=0的两侧，则m的取值范围是（ ）
| A、m＜-7或 m＞24 |
| B、m=7 或 m=24 |
| C、-7＜m＜24 |
| D、-24＜m＜7 |