题目内容
在△ABC中，已知a=5，b=4，∠C=60°，则C边长为（ ）
A、
| ||
B、
| ||
C、
| ||
| D、5 |
考点：余弦定理
专题：解三角形
分析：由题意和余弦定理直接求出边c的值即可．
解答：
解：由题意得，a=5，b=4，∠C=60°，
由余弦定理得，c2=a2+b2-2abcosC
=25+16-2×5×4×
=21，所以c=
，
故选：A．
由余弦定理得，c2=a2+b2-2abcosC
=25+16-2×5×4×
| 1 |
| 2 |
| 21 |
故选：A．
点评：本题考查余弦定理的应用，属于基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
已知命题①若a＞b，则
＜
，②若-2≤x≤0，则（x+2）（x-3）≤0，则下列说法正确的是（ ）
| 1 |
| a |
| 1 |
| b |
| A、①的逆命题为真 |
| B、②的逆命题为真 |
| C、①的逆否命题为真 |
| D、②的逆否命题为真 |
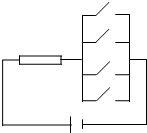某种开关在电路中闭合的概率为p，现将4只这种开关并联在某电路中（如图所示），若该电路为通路的概率为| 65 |
| 81 |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知点（3，1）和（-4，6）在直线3x-2y+m=0的两侧，则m的取值范围是（ ）
| A、m＜-7或 m＞24 |
| B、m=7 或 m=24 |
| C、-7＜m＜24 |
| D、-24＜m＜7 |