题目内容
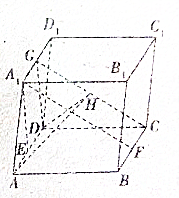如图，四棱柱ABCD=A1B1C1D1的底面是矩形，E，F，G，分别为AD，BC，A1D1的中点，A1E⊥平面ABCD，DH⊥CG，H为垂直（1）求证：A1F∥平面CDG
（2）求证：CG⊥平面ADH．
考点：直线与平面垂直的判定,直线与平面平行的判定
专题：证明题,空间位置关系与距离
分析：（1）连接EF，则四边形A1GCF为平行四边形，可得A1F∥CG，又EF∥CD，且EF∩A1F=F，CD∩CG=C，得平面A1EF∥平面GDC，可证CD∥A1F，从而可证A1F∥平面CDG．
（2）先证AD⊥平面A1EF，由A1F?平面A1EF，得AD⊥A1F，由（1）知：A1F∥CG，可得AD⊥CG，由DH⊥CG，DH∩AD=D，从而可证CG⊥平面ADH．
（2）先证AD⊥平面A1EF，由A1F?平面A1EF，得AD⊥A1F，由（1）知：A1F∥CG，可得AD⊥CG，由DH⊥CG，DH∩AD=D，从而可证CG⊥平面ADH．
解答：
证明：（1）如图，连接EF，则∵四棱柱ABCD=A1B1C1D1的底面是矩形，E，F，G，分别为AD，BC，A1D1的中点，
∴A1G
ED=CF，即四边形A1GCF为平行四边形．
∴A1F∥CG，
又∵EF∥CD，且EF∩A1F=F，CD∩CG=C，
∴平面A1EF∥平面GDC，
∴CD∥A1F，CD∩CG=C，
∴A1F∥平面CDG．
（2）∵四棱柱ABCD=A1B1C1D1的底面是矩形，A1E⊥平面ABCD，E，F，G，分别为AD，BC，A1D1的中点，
∴AD⊥A1E，EF⊥AD，AD∩A1E=A，
∴AD⊥平面A1EF，
∵A1F?平面A1EF，
∴AD⊥A1F，
∵由（1）知：A1F∥CG，
∴AD⊥CG，
∵DH⊥CG，DH∩AD=D，
∴CG⊥平面ADH．
证明：（1）如图，连接EF，则∵四棱柱ABCD=A1B1C1D1的底面是矩形，E，F，G，分别为AD，BC，A1D1的中点，∴A1G
| ∥ |
. |
∴A1F∥CG，
又∵EF∥CD，且EF∩A1F=F，CD∩CG=C，
∴平面A1EF∥平面GDC，
∴CD∥A1F，CD∩CG=C，
∴A1F∥平面CDG．
（2）∵四棱柱ABCD=A1B1C1D1的底面是矩形，A1E⊥平面ABCD，E，F，G，分别为AD，BC，A1D1的中点，
∴AD⊥A1E，EF⊥AD，AD∩A1E=A，
∴AD⊥平面A1EF，
∵A1F?平面A1EF，
∴AD⊥A1F，
∵由（1）知：A1F∥CG，
∴AD⊥CG，
∵DH⊥CG，DH∩AD=D，
∴CG⊥平面ADH．
点评：本题主要考查了直线与平面垂直的判定，直线与平面平行的判定，考查了空间想象能力、推理论证能力，考查了转化思想，属于中档题．
练习册系列答案
相关题目
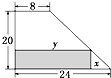（函数的应用）某厂有许多形状为直角梯形的铁皮边角料（如图），为降低消耗，开源节流，现要从这些边角料上截取矩形铁片（如图阴影部分）备用，则截取的矩形面积的最大值为