题目内容
2.矩形ABCD沿BD将△BCD折起,使C点在平面ABD上投影在AB上,折起后下列关系:①△ABC是直角三角形;②△ACD是直角三角形;③AD∥BC;④AD⊥BC.其中正确的是( )| A. | ①②④ | B. | ②③ | C. | ①③④ | D. | ②④ |
分析 记折起后C记为P点,根据线面垂直的性质定理和判断定理,分析折起后的线面,线线关系,可得答案.
解答 解:已知如图:折起后C记为P点,
由P(C)O⊥底面ABD,可得P(C)O⊥AD,
又由AB⊥AD,
可得:AD⊥平面P(C)AB,
进而AD⊥P(C)B,
又由PD(CD)⊥PB(CB),
故PB(CB)⊥平面P(C)AD,
故PB(CB)⊥P(C)A,
即:△ABP是直角三角形;
即:△ABC是直角三角形;
故①正确;
由①中,AD⊥平面P(C)AB,
可得:AD⊥P(C)A,
即②△APD是直角三角形,
即△ACD是直角三角形,
故②正确;
AD与BC,异面,故③错误;
由①中,AD⊥平面P(C)AB,
可得:AD⊥P(C)B,
即AD⊥BC,
故④正确;
故选:A
点评 本题以命题的真假判断与应用为载体,考查了空间直线与直线的位置关系,直线与平面的位置关系等知识点,难度中档.

练习册系列答案
相关题目
13.已知函数$f(x)=\left\{\begin{array}{l}-2x,x<0\\-{x^2}+2x,x≥0\end{array}\right.$若关于x的方程$f(x)=\frac{1}{2}x+m$恰有三个不相等的实数解,则m的取值范围是( )
| A. | $[{0,\frac{3}{4}}]$ | B. | $(0,\frac{3}{4})$ | C. | $[{0,\frac{9}{16}}]$ | D. | $(0,\frac{9}{16})$ |

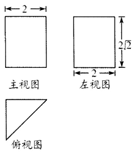 《九章算术》中将底面是直角三角形的直三棱柱称之为“堑堵”,已知某“堑堵”的三视图如图所示,则该“堑堵”的外接球的表面积为16π.
《九章算术》中将底面是直角三角形的直三棱柱称之为“堑堵”,已知某“堑堵”的三视图如图所示,则该“堑堵”的外接球的表面积为16π.