题目内容
7.已知M是抛物线C:y2=2px(p>0)上一点,F是抛物线的焦点,∠MFx=60°且|FM|=4.(I)求抛物线C的方程;
(II)已知D(-1,0),过F的直线l交抛物线C与A、B两点,以F为圆心的圆F与直线AD相切,试判断圆F与直线BD的位置关系,并证明你的结论.
分析 (I)证明△MNF为等边三角形,即可求抛物线C的方程;
(II)分类讨论,证明F到直线BD的距离等于圆F的半径,即可得出结论.
解答 解:(I)抛物线C:y2=2px(p>0)的准线方程为l′:x=-$\frac{p}{2}$,过M作MN⊥l′于点N,连接NF,则|MN|=|FM|,
∵∠NMF=∠MFx=60°,∴△MNF为等边三角形,
∴|NF|=4,∴p=2,
∴抛物线C的方程为y2=4x;
(II)直线l的斜率不存在时,△ABD为等腰三角形,且|AD|=|BD|.
∴圆F与直线BD相切;
直线l的斜率存在时,设方程为y=k(x-1),代入抛物线方程,得k2x2-(2k2+4)x+k2=0,
设A(x1,y1),B(x2,y2),则x1x2=1,∴x1=$\frac{1}{{x}_{2}}$,
直线AD的方程为y=$\frac{{y}_{1}}{{x}_{1}+1}$(x+1),即y1x-(x1+1)y+y1=0,
∴R2=$\frac{4{k}^{2}}{{k}^{2}+(\frac{1+{x}_{2}}{1-{x}_{2}})^{2}}$,
直线BD的方程为y2x-(x2+1)y+y2=0,
F到直线BD的距离d,d2=$\frac{4{{y}_{2}}^{2}}{{{y}_{2}}^{2}+({x}_{2}+1)^{2}}$=$\frac{4{k}^{2}}{{k}^{2}+(\frac{1+{x}_{2}}{1-{x}_{2}})^{2}}$,
∴R2=d2,
∴R=d,
∴圆F与直线BD相切,
综上所述,圆F与直线BD相切.
点评 本题考查抛物线的方程,考查直线与抛物线的位置关系,考查直线与圆的位置关系,属于中档题.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
17.某四棱锥的三视图如图所示,则该四棱锥的体积是( )


| A. | 36 | B. | 24 | C. | 12 | D. | 6 |
15.sin390°等于( )
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | -$\frac{\sqrt{3}}{2}$ |
2.矩形ABCD沿BD将△BCD折起,使C点在平面ABD上投影在AB上,折起后下列关系:①△ABC是直角三角形;②△ACD是直角三角形;③AD∥BC;④AD⊥BC.其中正确的是( )
| A. | ①②④ | B. | ②③ | C. | ①③④ | D. | ②④ |
12.设α,β是两个不同的平面,l,m是两条不同的直线,且l?α,m?β下面命题正确的是( )
| A. | 若l∥β,则α∥β | B. | 若α⊥β,则l⊥m | C. | 若l⊥β,则α⊥β | D. | 若α∥β,则l∥m |
19.已知函数f(x)的图象如图所示,则该函数的定义域、值域分别是( )
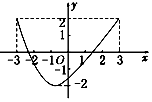

| A. | (-3,3),(-2,2) | B. | [-2,2],[-3,3] | C. | [-3,3],[-2,2] | D. | (-2,2),(-3,3) |
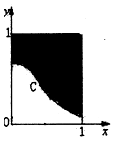 在如图所示的正方形中随机投掷10000个点,则落入阴影部分(曲线C为正态分布N(0,1)的密度曲线)的点的个数的估计值为( )
在如图所示的正方形中随机投掷10000个点,则落入阴影部分(曲线C为正态分布N(0,1)的密度曲线)的点的个数的估计值为( ) 已知椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{\sqrt{3}}{2}$,且过点($\frac{\sqrt{3}}{2}$,$\frac{1}{4}$).
已知椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{\sqrt{3}}{2}$,且过点($\frac{\sqrt{3}}{2}$,$\frac{1}{4}$).