题目内容
13.已知函数$f(x)=\left\{\begin{array}{l}-2x,x<0\\-{x^2}+2x,x≥0\end{array}\right.$若关于x的方程$f(x)=\frac{1}{2}x+m$恰有三个不相等的实数解,则m的取值范围是( )| A. | $[{0,\frac{3}{4}}]$ | B. | $(0,\frac{3}{4})$ | C. | $[{0,\frac{9}{16}}]$ | D. | $(0,\frac{9}{16})$ |
分析 若关于x的方程f(x)=$\frac{1}{2}$x+m恰有三个不相等的实数解,则函数f(x)的图象与直线y=$\frac{1}{2}$x+m有三个交点,数形结合可得答案.
解答 解:函数$f(x)=\left\{\begin{array}{l}-2x,x<0\\-{x^2}+2x,x≥0\end{array}\right.$的图象如下图所示: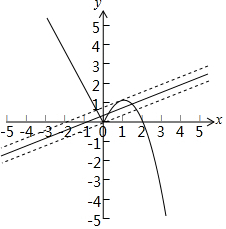
若关于x的方程f(x)=$\frac{1}{2}$x+m恰有三个不相等的实数解,
则函数f(x)的图象与直线y=$\frac{1}{2}$x+m有三个交点,
当直线y=$\frac{1}{2}$x+m经过原点时,m=0,
由y=-x2+2x的导数y′=-2x+2=$\frac{1}{2}$得:x=$\frac{3}{4}$,
当直线y=$\frac{1}{2}$x+m与y=-x2+2x相切时,切点坐标为:($\frac{3}{4}$,$\frac{15}{16}$),
当直线y=$\frac{1}{2}$x+m经过($\frac{3}{4}$,$\frac{15}{16}$)时,m=$\frac{9}{16}$,
故m∈(0,$\frac{9}{16}$),
故选:D.
点评 本题考查的知识点是根的存在性及根的个数判断,数形结合思想,难度中档.

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
3.已知抛物线y2=2px(p>0)上一点M到焦点F的距离等于3p,则直线MF的斜率为( )
| A. | ±$\sqrt{5}$ | B. | ±1 | C. | +$\frac{5}{2}$ | D. | ±$\frac{\sqrt{5}}{2}$ |
4.在公差为d的等差数列{an}中,“d>1”是“{an}是递增数列”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
8.双曲线$\frac{{x}^{2}}{2}$-$\frac{{y}^{2}}{12}$=1的离心率为( )
| A. | 2$\sqrt{3}$ | B. | $\sqrt{7}$ | C. | $\sqrt{3}$ | D. | 3 |
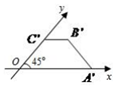 一直角梯形的直观图是一个如图所示的梯形,且OA′=2,B′C′=OC′=1,则该直角梯形的面积为( )
一直角梯形的直观图是一个如图所示的梯形,且OA′=2,B′C′=OC′=1,则该直角梯形的面积为( )