题目内容
17.设函数y=2sin(2x-$\frac{π}{3}$)的图象关于点P(x0,0)成中心对称,若x0∈[-$\frac{π}{2}$,0],则x0=-$\frac{π}{3}$.分析 求出函数的对称中心,结合x0∈[-$\frac{π}{2}$,0],求出x0的值.
解答 解:由于函数y=2sin(2x-$\frac{π}{3}$)的图象关于点P(x0,0)成中心对称,
所以2x0-$\frac{π}{3}$=kπ,k∈Z;
所以x0=$\frac{kπ}{2}$+$\frac{π}{6}$,k∈Z,
因为x0∈[-$\frac{π}{2}$,0],所以x0=-$\frac{π}{3}$.
故答案为-$\frac{π}{3}$.
点评 本题是基础题,考查三角函数的对称性,对称中心的求法,注意范围的应用,考查计算能力.

练习册系列答案
相关题目
8.双曲线$\frac{{x}^{2}}{2}$-$\frac{{y}^{2}}{12}$=1的离心率为( )
| A. | 2$\sqrt{3}$ | B. | $\sqrt{7}$ | C. | $\sqrt{3}$ | D. | 3 |
 如图,在四棱锥P-ABCD中,底面ABCD为矩形,平面PCD⊥平面ABCD,BC=1,AB=2,$PC=PD=\sqrt{2}$,E为PA中点.
如图,在四棱锥P-ABCD中,底面ABCD为矩形,平面PCD⊥平面ABCD,BC=1,AB=2,$PC=PD=\sqrt{2}$,E为PA中点.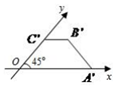 一直角梯形的直观图是一个如图所示的梯形,且OA′=2,B′C′=OC′=1,则该直角梯形的面积为( )
一直角梯形的直观图是一个如图所示的梯形,且OA′=2,B′C′=OC′=1,则该直角梯形的面积为( )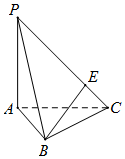 如图,在三棱锥P-ABC中,PA⊥平面ABC,AB=BC,PA=AC,E为PC上的动点,当 BE⊥PC时,$\frac{CE}{PC}$的值为$\frac{1}{4}$.
如图,在三棱锥P-ABC中,PA⊥平面ABC,AB=BC,PA=AC,E为PC上的动点,当 BE⊥PC时,$\frac{CE}{PC}$的值为$\frac{1}{4}$.