题目内容
设函数
=(cos(2x+
),sinx),
=(1,sinx),f(x)=
•
,
(Ⅰ)求函数f(x)最小正周期;
(Ⅱ)设△ABC的三个内角A、B、C的对应边分别是a、b、c,若c=
,cosB=
,f(
)=-
,求b.
| a |
| π |
| 3 |
| b |
| a |
| b |
(Ⅰ)求函数f(x)最小正周期;
(Ⅱ)设△ABC的三个内角A、B、C的对应边分别是a、b、c,若c=
| 6 |
| 1 |
| 3 |
| C |
| 2 |
| 1 |
| 4 |
考点:三角函数中的恒等变换应用,平面向量数量积的运算
专题:三角函数的图像与性质
分析:(Ⅰ)由条件利用两个向量的数量积公式,三角函数的恒等变换,求得函数f(x)=
-
sin2x,可得它的周期.
(Ⅱ)△ABC中,由f(
)=-
,求得sinC=
.再由正弦定理可得
=
求得b的值.
| 1 |
| 2 |
| ||
| 2 |
(Ⅱ)△ABC中,由f(
| C |
| 2 |
| 1 |
| 4 |
| ||
| 2 |
| b |
| sinB |
| c |
| sinC |
解答:
解:(Ⅰ)由题意可得函数f(x)=
•
=cos(2x+
)+sinx•sinx=
-
sin2x,
故函数的最小正周期为
=π.
(Ⅱ)△ABC中,∵c=
,cosB=
,∴sinB=
.
∵f(
)=-
=
-
sinC,∴sinC=
.
再由正弦定理可得
=
,即
=
,求得b=
.
| a |
| b |
| π |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
故函数的最小正周期为
| 2π |
| 2 |
(Ⅱ)△ABC中,∵c=
| 6 |
| 1 |
| 3 |
2
| ||
| 3 |
∵f(
| C |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
再由正弦定理可得
| b |
| sinB |
| c |
| sinC |
| b | ||||
|
| ||||
|
| 8 |
| 3 |
点评:本题主要考查两个向量的数量积公式,三角函数的恒等变换及化简求值,三角函数的周期性和求法,正弦定理的应用,属于基础题.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
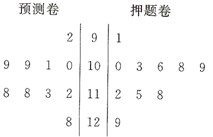 安徽某所学校高三年级有10名同学参加2014年北约自主招生,学校对这10名同学进行了辅导,并进行了两次模拟考试,检测成绩的茎叶图如图所示.
安徽某所学校高三年级有10名同学参加2014年北约自主招生,学校对这10名同学进行了辅导,并进行了两次模拟考试,检测成绩的茎叶图如图所示. 某校从参加高一年级期末考试的学生中抽出60名学生,将其成绩(均为整数)分成六段(即六组)[40,50),[50,60),…[90,100]后,画出如图部分频率分布直方图.请根据图形的信息,回答下列问题:
某校从参加高一年级期末考试的学生中抽出60名学生,将其成绩(均为整数)分成六段(即六组)[40,50),[50,60),…[90,100]后,画出如图部分频率分布直方图.请根据图形的信息,回答下列问题: 已知|
已知|