题目内容
13.数列{an}中,a1=1,前n项和是Sn,Sn=2an-1,n∈N*.(1)求a2,a3,a4;
(2)求通项公式an;
(3)求证:SnSn+2<Sn+12.
分析 (1)由Sn=2an-1,n∈N*.分别取n=2,3,4,即可得出.
(2)利用递推关系即可得出.
(3)利用(2),通过作差即可证明.
解答 解:(1)∵a1=1,Sn=2an-1,
∴当n=2时,a1+a2=2a2-1,∴a2=2
当n=3时,a1+a2+a3=2a3-1,∴a3=4
当n=4时,a1+a2+a3+a4=2a4-1,∴a4=8.
(2)∵Sn=2an-1,n∈N*①
∴Sn-1=2an-1-1,n≥2,n∈N*②
①-②得:an=2an-2an-1(n≥2,n∈N*),即an=2an-1(n≥2,n∈N*),
∴数列{an}是以1为首项,2为公比的等比数列,其通项公式${a_n}={2^{n-1}}$.
(3)证明:${S_n}=2{a_n}-1={2^n}-1$,
${S_n}{S_{n+2}}=({2^n}-1)({2^{n+2}}-1)={2^{2n+2}}-{2^{n+2}}-{2^n}+1$,
$S_{n+1}^2={({2^{n+1}}-1)^2}={2^{2n+2}}-{2^{n+2}}+1$,
∴$S_{n+1}^2-{S_n}{S_{n+2}}={2^n}>0$,∴${S_n}{S_{n+2}}<S_{n+1}^2$.
点评 本题考查了等比数列的通项公式、数列递推关系、作差法、数列递推关系,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案
相关题目
1.在圆x2+y2=4上任取一点P,过点P作x轴的垂线段PD,D为垂足,线段PD中点为M,当点P在圆上运动时,点M到直线l:x-y+1=0距离最大值为( )
| A. | $\frac{{\sqrt{10}+\sqrt{2}}}{2}$ | B. | $\frac{{\sqrt{10}-\sqrt{2}}}{2}$ | C. | $\frac{{3\sqrt{2}}}{2}$ | D. | $\frac{{\sqrt{2}}}{2}$ |
18.某同学用“五点法”画函数f(x)=Asin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)在某一周期内的图象时,列表并填入部分数据,如表:
(1)请将上表数据补充完整,填写在答题卡相应的位置,并求f(x)的解析式;
(2)将函数f(x)的图象上每一点的纵坐标缩短到原来的$\frac{1}{2}$倍,横坐标不变,得到函数g(x)的图象.试求g(x)在区间[π,$\frac{5π}{2}$]上的最值.
(1)请将上表数据补充完整,填写在答题卡相应的位置,并求f(x)的解析式;
(2)将函数f(x)的图象上每一点的纵坐标缩短到原来的$\frac{1}{2}$倍,横坐标不变,得到函数g(x)的图象.试求g(x)在区间[π,$\frac{5π}{2}$]上的最值.
| ωx+φ | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π |
| x | 2π | $\frac{13π}{2}$ | |||
| f(x) | 0 | 4 | -4 | 0 |
2.已知全集U=R,A={x|-2≤x≤4},B={x|-3≤x≤3},求(∁UA)∩(∁UB)=( )
| A. | {x|-2≤x≤3} | B. | {x|x<-2或x>4} | C. | {x|-3≤x≤4} | D. | {x|x<-3或x>4} |
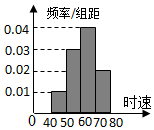 关于统计数据的分析,有以下几个结论:
关于统计数据的分析,有以下几个结论: