题目内容
9.在△ABC中,$\overrightarrow{AB}$=2$\overrightarrow{a}$,$\overrightarrow{AC}$=3$\overrightarrow{b}$,设P为BC边上任意一点,若$\overrightarrow{AP}$=$λ\overrightarrow{a}$+$μ\overrightarrow{b}$,则λμ的最大值为( )| A. | $\frac{2}{3}$ | B. | $\frac{3}{2}$ | C. | $\frac{1}{6}$ | D. | 6 |
分析 用$\overrightarrow{AB},\overrightarrow{AC}$表示$\overrightarrow{AP}$,根据三点共线原理得出λ,μ的关系,使用基本不等式得出得出λμ的最大值.
解答 解:∵$\overrightarrow{AB}$=2$\overrightarrow{a}$,$\overrightarrow{AC}$=3$\overrightarrow{b}$,∴$\overrightarrow{AP}$=$\frac{λ}{2}\overrightarrow{AB}$+$\frac{μ}{3}\overrightarrow{AC}$.∵P为BC边上任意一点,∴$\frac{λ}{2}$+$\frac{μ}{3}$=1,
∴1≥2$\sqrt{\frac{λμ}{6}}$,∴λμ≤$\frac{3}{2}$.
故选:B.
点评 本题考查了平面向量的基本定理,共线原理,基本不等式,属于中档题.

练习册系列答案
相关题目
19.在5张电话卡中,有3张移动卡和2张联通卡,从中任取2张,若事件“2张全是移动卡”的概率是$\frac{3}{10}$,那么概率是$\frac{7}{10}$的事件是( )
| A. | 至多有一张移动卡 | B. | 恰有一张移动卡 | ||
| C. | 都不是移动卡 | D. | 至少有一张移动卡 |
19.经过两点$A({m,\sqrt{3}})$,$B({-m,-\sqrt{3}m})$的直线的倾斜角为30°,则m=( )
| A. | -3 | B. | $-\frac{3}{5}$ | C. | $-\frac{1}{3}$ | D. | 1 |
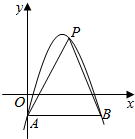 姐图,在平面直角坐标系中,抛物线y=-(x-2)2+3与y轴交于点A,过点A与x轴平行的直线交抛物线于另一点B,点P是直线AB上方的抛物线上一点,设点P的横坐标为m,则△PAB的面积S的取值范围为0<S≤8.
姐图,在平面直角坐标系中,抛物线y=-(x-2)2+3与y轴交于点A,过点A与x轴平行的直线交抛物线于另一点B,点P是直线AB上方的抛物线上一点,设点P的横坐标为m,则△PAB的面积S的取值范围为0<S≤8.