题目内容

4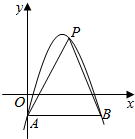．姐图，在平面直角坐标系中，抛物线y=-（x-2）2+3与y轴交于点A，过点A与x轴平行的直线交抛物线于另一点B，点P是直线AB上方的抛物线上一点，设点P的横坐标为m，则△PAB的面积S的取值范围为0＜S≤8．

分析 表示出P点坐标，进而表示出△PAB的底与高的长度，即可得出S与m的关系式，利用配方法可得△PAB的面积S的取值范围．

解答 解：由题意，P点坐标为：（m，-（m-2）2+3）
由题意可得出：AB=4，P到AB的距离为-（m-2）2+4，
∴S=$\frac{1}{2}$×4×[-（m-2）2+4]=-2（m-2）2+8；
∵0＜m＜4，∴0＜S≤8．
故答案为：0＜S≤8．

点评 此题主要考查了二次函数的综合应用以及三角形面积求法和图象上点的坐标性质，根据P点坐标得出P到AB的距离是解题关键．

练习册系列答案
相关题目
14．已知复数z满足z（1-$\sqrt{3}$i）=4（i为虚数单位），则z=（　　）
A．-2-2$\sqrt{3}$iB．1+$\sqrt{3}$iC．-1-$\sqrt{3}$iD．1-$\sqrt{3}$i
15．节日前夕，小明的妈妈给小明买了两只可以装电池的发光玩具狗．这两只玩具狗在装满电池后，都会在打开电开关后的4秒内任一时刻等可能发光，然后每只发光玩具狗以4秒为间隔闪亮．那么，当这两只发光玩具狗同时打开电开关后，求它们第一次闪亮的时刻相差不超过2秒的概率．
12．从点（2，0）引圆x2+y2=1的切线，则切线长为$\sqrt{3}$．
19．对数函数f（x）的图象过点（3，-2），则f（$\sqrt{3}$）=-1．
9．在△ABC中，$\overrightarrow{AB}$=2$\overrightarrow{a}$，$\overrightarrow{AC}$=3$\overrightarrow{b}$，设P为BC边上任意一点，若$\overrightarrow{AP}$=$λ\overrightarrow{a}$+$μ\overrightarrow{b}$，则λμ的最大值为（　　）
A．$\frac{2}{3}$B．$\frac{3}{2}$C．$\frac{1}{6}$D．6
16．已知在数列{an}中，a1=1，当n≥2时，其前n项和Sn满足Sn2-anSn+2an=0．
（1）求数列{an}的通项公式；
（2）若bn=2n-1，记数列{$\frac{1}{{S}_{n}{b}_{n}}$}的前n项和为Tn，求Tn．
13．已知等差数列{an}的首项a1=1，公差d＞0，且a2，a5，a14成等比数列．
（Ⅰ） 求数列{an}的通项公式；
（Ⅱ） 令${b_n}=\frac{1}{{{a_n}•{a_{n+1}}}}+{a_n}$，求数列{bn}的前n项和Sn．
14．在如图的电路图中，“开关A的闭合”是“灯泡B亮”的（　　）
A．充分非必要条件B．必要非充分条件
C．充要条件D．既非充分又非必要条件

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网