题目内容
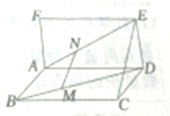如图所示，已知矩形ABCD和矩形ADEF所在的平面相互垂直，点MN分别在对角线BDAE上，且BM=| 1 |
| 3 |
| 1 |
| 3 |
| MN |
| CD |
| DE |
考点：共线向量与共面向量
专题：作图题,空间位置关系与距离
分析：由题意，在AD上取点G，使AG=
AD，从而可证GM∥CD，GN∥DE，从而可证向量
，
，
共面．
| 1 |
| 3 |
| MN |
| CD |
| DE |
解答：
证明：如图，在AD上取点G，使AG=
AD，
又∵BM=
BD，
∴GM∥AB，又∵AB∥CD，
∴GM∥CD，
同理，GN∥DE，
故由GN、GM、MN共面可知，
向量
，
，
共面．
证明：如图，在AD上取点G，使AG=| 1 |
| 3 |
又∵BM=
| 1 |
| 3 |
∴GM∥AB，又∵AB∥CD，
∴GM∥CD，
同理，GN∥DE，
故由GN、GM、MN共面可知，
向量
| MN |
| CD |
| DE |
点评：本题考查了向量的概念及线线平行的证明，属于中档题．
练习册系列答案
相关题目
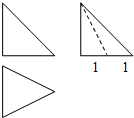一空间几何体的三视图如图所示，其中正视图和侧视图都是腰长为2的等腰直角三角形，则该几何体的侧面积为