题目内容
已知Sn=na1+
d,求证:{an}是等差数列.
| n(n-1) |
| 2 |
考点:等差关系的确定
专题:等差数列与等比数列
分析:当n=1时,a1=S1=a1.当n≥2时,an=Sn-Sn-1=a1+(n-1)d,只要证明an-an-1=常数即可.,
解答:
证明:当n=1时,a1=S1=a1.
当n≥2时,an=Sn-Sn-1=na1+
d-[(n-1)a1+
d]
=a1+(n-1)d,
∴an-an-1=d,
∴数列{an}是等差数列.
当n≥2时,an=Sn-Sn-1=na1+
| n(n-1) |
| 2 |
| (n-1)(n-2) |
| 2 |
=a1+(n-1)d,
∴an-an-1=d,
∴数列{an}是等差数列.
点评:本题考查了等差数列的定义通项公式及其前n项和公式,属于基础题.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
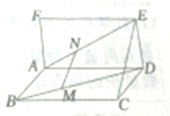 如图所示,已知矩形ABCD和矩形ADEF所在的平面相互垂直,点MN分别在对角线BDAE上,且BM=
如图所示,已知矩形ABCD和矩形ADEF所在的平面相互垂直,点MN分别在对角线BDAE上,且BM=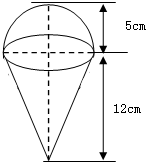 如图,一个圆锥形的空杯子上面放着一个半球形的冰淇淋,假设冰淇淋融化后体积不变,是否会溢出杯子?请说明理由.请用你的计算数据说明理由.(冰、水的体积差异忽略不计)(π取3.14)
如图,一个圆锥形的空杯子上面放着一个半球形的冰淇淋,假设冰淇淋融化后体积不变,是否会溢出杯子?请说明理由.请用你的计算数据说明理由.(冰、水的体积差异忽略不计)(π取3.14) 如图,已知在正方体ABCD-A1B1C1D1中,面对角线A1B、BC1的中点为E、F,求证:EF∥平面ABCD.
如图,已知在正方体ABCD-A1B1C1D1中,面对角线A1B、BC1的中点为E、F,求证:EF∥平面ABCD. (Ⅰ) 如图,一个扇形OAB的面积是1cm2,它的周长是4cm,求圆心角的弧度数和弦长AB.
(Ⅰ) 如图,一个扇形OAB的面积是1cm2,它的周长是4cm,求圆心角的弧度数和弦长AB.