题目内容
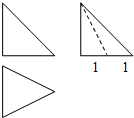 一空间几何体的三视图如图所示,其中正视图和侧视图都是腰长为2的等腰直角三角形,则该几何体的侧面积为
一空间几何体的三视图如图所示,其中正视图和侧视图都是腰长为2的等腰直角三角形,则该几何体的侧面积为考点:由三视图求面积、体积
专题:空间位置关系与距离
分析:根据几何体的三视图得出该几何体是底面为等腰三角形,高为2的三棱锥,求出它的侧面积即可.
解答:
解:根据几何体的三视图得,
该几何体是底面是等腰三角形,高为2的三棱锥,如图所示;
∴该三棱锥的侧面积是
S侧=
×2×2+2×
×
×
=2+2×
×2
×
=2+2
.
故答案为:2+2
.
该几何体是底面是等腰三角形,高为2的三棱锥,如图所示;

∴该三棱锥的侧面积是
S侧=
| 1 |
| 2 |
| 1 |
| 2 |
| 22+22 |
(22+12)-(
|
=2+2×
| 1 |
| 2 |
| 2 |
| 3 |
=2+2
| 6 |
故答案为:2+2
| 6 |
点评:本题考查了空间三视图的应用问题,解题的关键是根据几何体的三视图得出几何体是什么图形,是基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知f(x)是定义在(-∞,+∞)上的偶函数,且在(-∞,0]上是减函数,设a=f(log4(
)),b=f(log2(
)),c=f(21.1),则a,b,c的大小关系是( )
| 1 |
| 7 |
| 1 |
| 3 |
| A、c<a<b |
| B、c<b<a |
| C、b<c<a |
| D、a<b<c |
已知函数f(x)=
,若对于任意a,b,c∈R,都有f(a)+f(b)>f(c)成立,则实数m的取值范围是( )
| ex+m |
| ex+1 |
A、[
| ||
| B、[0,1] | ||
| C、[1,2] | ||
D、[
|
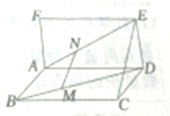 如图所示,已知矩形ABCD和矩形ADEF所在的平面相互垂直,点MN分别在对角线BDAE上,且BM=
如图所示,已知矩形ABCD和矩形ADEF所在的平面相互垂直,点MN分别在对角线BDAE上,且BM=