题目内容
已知
+
=1，（a＞0，b＞0）点（0，b）到直线x-2y-a=0的距离的最小值为 ．
| 1 |
| a |
| 2 |
| b |
考点：基本不等式
专题：不等式的解法及应用
分析：写出点（0，b）到直线x-2y-a=0的距离，去绝对值后结合
+
=1，然后利用基本不等式求最值．
| 1 |
| a |
| 2 |
| b |
解答：
解：点（0，b）到直线x-2y-a=0的距离为
=
|a+2b|=
(a+2b)，
∵
+
=1，
∴
(a+2b)=
(a+2b)(
+
)=
(1+4+
+
)≥
(5+2
)=
．
当且仅当
，即a=b=3时等号成立．
∴点（0，b）到直线x-2y-a=0的距离的最小值为
．
故答案为：
．
| |-2b-a| | ||
|
| ||
| 5 |
| ||
| 5 |
∵
| 1 |
| a |
| 2 |
| b |
∴
| ||
| 5 |
| ||
| 5 |
| 1 |
| a |
| 2 |
| b |
| ||
| 5 |
| 2b |
| a |
| 2a |
| b |
| ||
| 5 |
|
9
| ||
| 5 |
当且仅当
|
∴点（0，b）到直线x-2y-a=0的距离的最小值为
9
| ||
| 5 |
故答案为：
9
| ||
| 5 |
点评：本题考查了点到直线的距离，考查了基本不等式求最值，是基础题．
练习册系列答案
相关题目
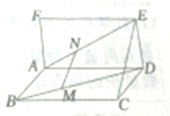如图所示，已知矩形ABCD和矩形ADEF所在的平面相互垂直，点MN分别在对角线BDAE上，且BM=