题目内容
已知在平面直角坐标系中,O为坐标原点,给定两点A(1,0),B(0,-2),点C满足
=α
+β
,其中α,β∈R,且α-2β=1.
(1)求点C的轨迹方程;
(2)设点C的轨迹与双曲线
-y2=13,(a>0)交于两点M,N,且OM⊥ON,求该双曲线的方程.
| OC |
| OA |
| OB |
(1)求点C的轨迹方程;
(2)设点C的轨迹与双曲线
| x2 |
| a2 |
考点:双曲线的简单性质
专题:向量与圆锥曲线
分析:(1)由向量等式,得点C的坐标,消去参数即得点C的轨迹方程;
(2)联立直线方程和双曲线方程,化为关于x的一元二次方程利用根与系数关系得到M,N两点的横纵坐标的积,把OM⊥ON转化为向量数量积求得a2,则双曲线方程可求.
(2)联立直线方程和双曲线方程,化为关于x的一元二次方程利用根与系数关系得到M,N两点的横纵坐标的积,把OM⊥ON转化为向量数量积求得a2,则双曲线方程可求.
解答:
解:(1)设C(x,y),A(1,0),B(0,-2),由
=α
+β
,得
(x,y)=α(1,0)+β(0,-2),
∴
,即点C的轨迹方程为x+y=1;
(2)设M(x1,y1),N(x2,y2),
联立
,得(1-a2)x2+2a2x-14a2=0.
x1+x2=
,x1x2=
,
y1y2=(1-x1)(1-x2)=1-(x1+x2)+x1x2
=1-
+
=
=
.
∵OM⊥ON,
∴x1x2+y1y2=
+
=
=0.
即27a2-1=0,
∴a2=
.
∴双曲线的方程27x2-y2=13.
| OC |
| OA |
| OB |
(x,y)=α(1,0)+β(0,-2),
∴
|
(2)设M(x1,y1),N(x2,y2),
联立
|
x1+x2=
| 2a2 |
| a2-1 |
| 14a2 |
| a2-1 |
y1y2=(1-x1)(1-x2)=1-(x1+x2)+x1x2
=1-
| 2a2 |
| a2-1 |
| 14a2 |
| a2-1 |
| a2-1-2a2+14a2 |
| a2-1 |
| 13a2-1 |
| a2-1 |
∵OM⊥ON,
∴x1x2+y1y2=
| 14a2 |
| a2-1 |
| 13a2-1 |
| a2-1 |
| 27a2-1 |
| a2-1 |
即27a2-1=0,
∴a2=
| 1 |
| 27 |
∴双曲线的方程27x2-y2=13.
点评:本题考查了平面向量的数量积运算,考查了直线与圆锥曲线的关系,涉及直线与圆锥曲线的关系问题,常采用联立直线方程与圆锥曲线方程,借助于根与系数关系求解,是中档题.

练习册系列答案
相关题目
已知f(x)是定义在(-∞,+∞)上的偶函数,且在(-∞,0]上是减函数,设a=f(log4(
)),b=f(log2(
)),c=f(21.1),则a,b,c的大小关系是( )
| 1 |
| 7 |
| 1 |
| 3 |
| A、c<a<b |
| B、c<b<a |
| C、b<c<a |
| D、a<b<c |
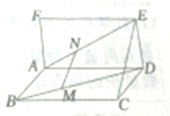 如图所示,已知矩形ABCD和矩形ADEF所在的平面相互垂直,点MN分别在对角线BDAE上,且BM=
如图所示,已知矩形ABCD和矩形ADEF所在的平面相互垂直,点MN分别在对角线BDAE上,且BM= 如图,已知在正方体ABCD-A1B1C1D1中,面对角线A1B、BC1的中点为E、F,求证:EF∥平面ABCD.
如图,已知在正方体ABCD-A1B1C1D1中,面对角线A1B、BC1的中点为E、F,求证:EF∥平面ABCD.