题目内容
已知椭圆C的一个顶点为(0,-1),焦点在x轴上,右焦点到直线x-y+1=0的距离为
.
(1)求椭圆C的方程;
(2)过点F(1,0)作直线l与椭圆C交于不同的两点A、B,
=λ
,T(2,0),λ∈[2,-1],求|
+
|的取值范围.
| 2 |
(1)求椭圆C的方程;
(2)过点F(1,0)作直线l与椭圆C交于不同的两点A、B,
| FA |
| FB |
| TA |
| TB |
考点:直线与圆锥曲线的关系,椭圆的标准方程
专题:计算题,平面向量及应用,直线与圆,圆锥曲线的定义、性质与方程
分析:(1)由题意的性质,可得b=1,再由点到直线的距离公式,可得c,再由a,b,c的关系,得到a,进而得到椭圆方程;
(2)设出直线方程,代入椭圆方程,利用韦达定理及向量知识,结合配方法,即可求|
+
|的取值范围.
(2)设出直线方程,代入椭圆方程,利用韦达定理及向量知识,结合配方法,即可求|
| TA |
| TB |
解答:
解:(1)椭圆C的一个顶点为(0,-1),
且焦点在x轴上,则b=1,
右焦点(c,0)到直线x-y+1=0的距离为
,
则
=
,
则c=1,则a2=b2+c2=2,
即有椭圆C的方程
+y2=1;
(2)由题意容易验证直线l的斜率不为0,故可设直线l的方程为x=ky+1,
代入椭圆方程
+y2=1中,得(k2+2)y2+2ky-1=0.
设A(x1,y1),B(x2,y2),由根与系数关系,得y1+y2=-
①,y1y2=-
②,
因为
=λ
,所以
=λ且λ<0,所以将上式①的平方除以②,得
+
+2=
,
即
=
,所以λ+
+2=
,
由λ∈[-2,-1],则-
≤λ+
≤-2,-
≤λ+
+2≤0,即-
≤
≤0,
即0≤k2≤
.
∵
=(x1-2,y1),
=(x2-2,y2),
∴
+
=(x1+x1-4,y1+y2),
又y1+y2=-
,x1+x2-4=k(y1+y2)-2=-
,
故|
+
|2=(x1+x2-4)2+(y1+y2)2=
+
=16-
+
.令t=
,由于0≤k2≤
.则
≤t≤
,
则|
+
|2=16-28t+8t2=8(t-
)2-
,
由于
≤t≤
,∴|
+
|2∈[4,
].
则|
+
|∈[2,
].
且焦点在x轴上,则b=1,
右焦点(c,0)到直线x-y+1=0的距离为
| 2 |
则
| |c-0+1| | ||
|
| 2 |
则c=1,则a2=b2+c2=2,
即有椭圆C的方程
| x2 |
| 2 |
(2)由题意容易验证直线l的斜率不为0,故可设直线l的方程为x=ky+1,
代入椭圆方程
| x2 |
| 2 |
设A(x1,y1),B(x2,y2),由根与系数关系,得y1+y2=-
| 2k |
| 2+k2 |
| 1 |
| 2+k2 |
因为
| FA |
| FB |
| y1 |
| y2 |
| y1 |
| y2 |
| y2 |
| y1 |
| -4k2 |
| 2+k2 |
即
| (y1+y2)2 |
| y1y2 |
| -4k2 |
| 2+k2 |
| 1 |
| λ |
| -4k2 |
| 2+k2 |
由λ∈[-2,-1],则-
| 5 |
| 2 |
| 1 |
| λ |
| 1 |
| 2 |
| 1 |
| λ |
| 1 |
| 2 |
| 4k2 |
| 2+k2 |
即0≤k2≤
| 2 |
| 7 |
∵
| TA |
| TB |
∴
| TA |
| TB |
又y1+y2=-
| 2k |
| 2+k2 |
| 4(1+k2) |
| 2+k2 |
故|
| TA |
| TB |
| 16(1+k2)2 |
| (2+k2)2 |
| 4k2 |
| (2+k2)2 |
=16-
| 28 |
| 2+k2 |
| 8 |
| (2+k2)2 |
| 1 |
| 2+k2 |
| 2 |
| 7 |
| 7 |
| 16 |
| 1 |
| 2 |
则|
| TA |
| TB |
| 7 |
| 4 |
| 17 |
| 2 |
由于
| 7 |
| 16 |
| 1 |
| 2 |
| TA |
| TB |
| 169 |
| 32 |
则|
| TA |
| TB |
13
| ||
| 8 |
点评:本题考查椭圆的标准方程,考查直线与椭圆的位置关系,考查向量知识的运用,考查韦达定理,考查学生的计算能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图是函数y=f(x)=Asin(ωx+φ)(A>0,ω>0)图象上的一段,则在区间(0,2π)上,使等式f(x)=f(0)成立的x的集合为
如图是函数y=f(x)=Asin(ωx+φ)(A>0,ω>0)图象上的一段,则在区间(0,2π)上,使等式f(x)=f(0)成立的x的集合为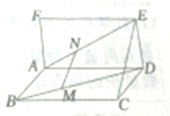 如图所示,已知矩形ABCD和矩形ADEF所在的平面相互垂直,点MN分别在对角线BDAE上,且BM=
如图所示,已知矩形ABCD和矩形ADEF所在的平面相互垂直,点MN分别在对角线BDAE上,且BM=