题目内容
已知a=(
)-
,b=(
)-
,c=(
)-
,则a,b,c三个数的大小关系是 .
| 3 |
| 5 |
| 1 |
| 3 |
| 3 |
| 5 |
| 1 |
| 2 |
| 4 |
| 3 |
| 1 |
| 2 |
考点:不等式比较大小
专题:函数的性质及应用
分析:利用指数函数的单调性,根据a,b同底,可比较a,b的大小,利用指数函数的运算性质,将a,c的指数部分化为一致,结合幂函数的单调性,可比较a,c的大小.
解答:
解:∵0<
<1,故函数y=(
)x为减函数
∵-
>-
故a=(
)-
<b=(
)-
∵-
<0,故函数y=(x)-
为减函数
又∵
<
,a=(
)-
,c=(
)-
∴a>c
故答案为:c<a<b
| 3 |
| 5 |
| 3 |
| 5 |
∵-
| 1 |
| 3 |
| 1 |
| 2 |
故a=(
| 3 |
| 5 |
| 1 |
| 3 |
| 3 |
| 5 |
| 1 |
| 2 |
∵-
| 1 |
| 6 |
| 1 |
| 6 |
又∵
| 9 |
| 25 |
| 64 |
| 27 |
| 9 |
| 25 |
| 1 |
| 6 |
| 64 |
| 27 |
| 1 |
| 6 |
∴a>c
故答案为:c<a<b
点评:本题考查的知识点是指数函数单调性和幂函数的单调性,熟练掌握利用函数单调性比较数大小的方法和技巧是解答的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知函数,f(x)=cosx,g(x)=-x2+4x-3,若存在实数a,b∈R,满足g(a)=f(b),则a的取值范围是( )
| A、[1,3] | ||||
| B、(1,3) | ||||
C、[2-
| ||||
D、(2-
|
一颗正方体骰子,共六个面的点数分别是1、2、3、4、5、6,将这颗骰子连续掷三次观察向上的点数,则三次点数和为16的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
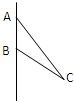 如图,在△ABC中,AB=3,BC=5,∠ABC=120°将△ABC绕直线AB旋转一周,则所形成的旋转体的侧面积是
如图,在△ABC中,AB=3,BC=5,∠ABC=120°将△ABC绕直线AB旋转一周,则所形成的旋转体的侧面积是