题目内容
下列函数中，在区间（0，+∞）内为减函数的是（ ）
| A、y=|x| | ||
| B、y=3x | ||
| C、y=-x2 | ||
D、y=-
|
考点：函数单调性的判断与证明
专题：函数的性质及应用
分析：利用特殊值法，结合减函数的定义易得结论．
解答：
解：由减函数的定义当x1＜x2，恒有f（x1）＞f（x2），
令x1=1，x2=2，则对于A，y1=1，y2=2，y1＜y2，与减函数的定义不符，故排除A；
对于B，y1=3，y2=6，y1＜y2，与减函数的定义不符，故排除B；
对于C，由y′=-2x得y=-x2在x∈（0，+∞）内为减函数，符号题意；
对于D，y1=-1，y2=-
，y1＜y2，与减函数的定义不符，故排除D；
故选：C．
令x1=1，x2=2，则对于A，y1=1，y2=2，y1＜y2，与减函数的定义不符，故排除A；
对于B，y1=3，y2=6，y1＜y2，与减函数的定义不符，故排除B；
对于C，由y′=-2x得y=-x2在x∈（0，+∞）内为减函数，符号题意；
对于D，y1=-1，y2=-
| 1 |
| 2 |
故选：C．
点评：本题利用函数单调性的定义，结合选择题的特点，利用特殊值加以判断，可以起到事半功倍的效果．
练习册系列答案
口算小状元口算速算天天练系列答案
相关题目
若0＜a＜1，则下列各式中正确的是（ ）
| A、loga（1-a）＞0 |
| B、a1-a＞1 |
| C、loga（1-a）＜0 |
| D、（1-a）2＞a2 |
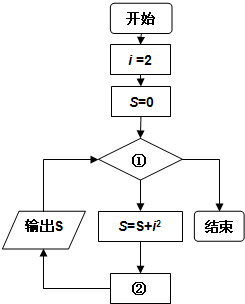如图是表示输出22，22+42，22+42+62，…，22+42+62+…+20042的值的过程的一个程序框图，那么在图中①、②处应分别填上（ ）| A、i≤2014，i=i+2 |
| B、i≤1007，i=i+2 |
| C、i≤2014，i=i+1 |
| D、i≤1007，i=i+1 |
已知三个不全相等的实数m，p，q成等比数列，则可能成等差数列的是（ ）
| A、m，p，q | ||||||
| B、m2，p2，q2 | ||||||
| C、m3，p3，q3 | ||||||
D、
|
若直线l上不同的三个点A，B，C与直线l外一点O，使得x2
+x
=2
成立，则满足条件的实数x的集合为（ ）
| OA |
| OB |
| BC |
| A、{-1，0} | ||||||||
B、{
| ||||||||
C、{
| ||||||||
| D、{-1} |
设Ω为平面直角坐标系xOy中的点集，从Ω中的任意一点P作x轴、y轴的垂线，垂足分别为M，N，记点M的横坐标的最大值与最小值之差为x（Ω），点N的纵坐标的最大值与最小值之差为y（Ω）．如果Ω是边长为1的正方形，那么x（Ω）+y（Ω）的取值范围是（ ）
A、[
| ||||
B、[2，2
| ||||
C、[1，
| ||||
D、[1，2
|
若不等式ax2+ax-1＜0对一切x∈R恒成立，则实数a的取值范围是（ ）
| A、（-∞，0） |
| B、（-∞，0] |
| C、（-4，0） |
| D、（-4，0] |