题目内容
已知抛物线C:y2=2px(p>0)过点A(2,-4),
(Ⅰ)求抛物线C的方程,并求其准线l的方程;
(Ⅱ)若点B(0,2),求过点B且与抛物线C有且仅有一个公共点的直线l的方程.
(Ⅰ)求抛物线C的方程,并求其准线l的方程;
(Ⅱ)若点B(0,2),求过点B且与抛物线C有且仅有一个公共点的直线l的方程.
考点:直线与圆锥曲线的关系,抛物线的标准方程,抛物线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:(Ⅰ)利用已知条件求出p,即可求抛物线C的方程,并求其准线l的方程;
(Ⅱ)①当直线l的斜率不存在时,②如果直线l的斜率为0,分别判断是否满足题意,③直线l的斜率存在且不为0,设直线l的方程为y=kx+2,联立直线与抛物线方程,利用△=0求出k,即可得到直线方程.
(Ⅱ)①当直线l的斜率不存在时,②如果直线l的斜率为0,分别判断是否满足题意,③直线l的斜率存在且不为0,设直线l的方程为y=kx+2,联立直线与抛物线方程,利用△=0求出k,即可得到直线方程.
解答:
解:( I)由题抛物线C:y2=2px(p>0)过点A(2,-4),16=4p,解得p=4,
抛物线C的方程为y2=8x,其准线l方程为x=-2; …(4分)
(Ⅱ)由题,①当直线l的斜率不存在时,y轴符合题意,其方程为x=0;
②如果直线l的斜率为0,y=2符合题意;
③如果直线l的斜率存在且不为0,则设直线l的方程为y=kx+2,
由
得ky2-8y+16=0,
由△=64-64k=0得k=1,故直线l的方程为y=x+2,即x-y+2=0,
因此,直线l的方程为x=0或y=2或x-y+2=0.(用其他方法解答的请酌情给分) …(12分)
抛物线C的方程为y2=8x,其准线l方程为x=-2; …(4分)
(Ⅱ)由题,①当直线l的斜率不存在时,y轴符合题意,其方程为x=0;
②如果直线l的斜率为0,y=2符合题意;
③如果直线l的斜率存在且不为0,则设直线l的方程为y=kx+2,
由
|
由△=64-64k=0得k=1,故直线l的方程为y=x+2,即x-y+2=0,
因此,直线l的方程为x=0或y=2或x-y+2=0.(用其他方法解答的请酌情给分) …(12分)
点评:本题考查抛物线的方程的求法,直线与抛物线的位置关系的应用,注意分类讨论思想的应用.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
给出四个函数,分别满足①f(x+y)=f(x)+f(y);②g(x+y)=g(x)•g(y);③ϕ(x•y)=ϕ(x)+ϕ(y);④ω(x•y)=ω(x)•ω(y),又给出四个函数的图象如下:
则正确的配匹方案是( )

则正确的配匹方案是( )
| A、①-M ②-N ③-P ④-Q |
| B、①-N ②-P ③-M ④-Q |
| C、①-P ②-M ③-N ④-Q |
| D、①-Q ②-M ③-N ④-P |
下列命题正确的是( )
| A、若a>b>1,c<0,则ae>be | ||||
| B、若|a|>b,则a2>b2 | ||||
C、?x0∈R,x0+
| ||||
D、若a>0,b>0且a+b=1,则
|
将边长为1的正方形ABCD沿对角线BD折成直二面角,若点P满足
=
-
+
,则|
|的值为( )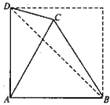
| BP |
| 1 |
| 2 |
| BA |
| 1 |
| 2 |
| BC |
| BD |
| BP |

A、
| ||||
| B、2 | ||||
C、
| ||||
D、
|
双曲线的一个焦点F(4,0)到渐近线的距离为2,则双曲线的离心率是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知f(x)是奇函数,且f(x+2)=f(x),当0≤x≤1时,f(x)=2x(1-x),则f(-
)=( )
| 5 |
| 2 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
| (lg9-1)2 |
| A、lg9-1 | ||
| B、1-lg9 | ||
| C、8 | ||
D、2
|