题目内容
将边长为1的正方形ABCD沿对角线BD折成直二面角，若点P满足
=
-
+
，则|
|的值为（ ）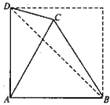
| BP |
| 1 |
| 2 |
| BA |
| 1 |
| 2 |
| BC |
| BD |
| BP |
A、
| ||||
| B、2 | ||||
C、
| ||||
D、
|
考点：向量在几何中的应用
专题：平面向量及应用
分析：将向量
，
，
看成基底，然后将向量
用基底表示出来，利用求模的方法直接计算即可．
| BA |
| BC |
| BD |
| BP |
解答：
解：如图，取BD的中点O，连接OA，OC，易知OC⊥BD，OA⊥BD．
因为正方形ABCD，结合已知得∠CBO=∠ABO=45°，易求得BA=AC=CB=1．BD=
．
所以△ABC是等边△．所以∠CBA=60°．
所以
=
-
+
=
(
-
)+
=
+
，
由正方体的性质可知，BD⊥CO，BD⊥AO，故BD⊥面ACO，所以AC⊥BD．
所以|
|2=|
+
|2=(
+
)2
=
2+
2+
•
=
×1+2+0=
．
故|
|=
．
故选A
解：如图，取BD的中点O，连接OA，OC，易知OC⊥BD，OA⊥BD．因为正方形ABCD，结合已知得∠CBO=∠ABO=45°，易求得BA=AC=CB=1．BD=
| 2 |
所以△ABC是等边△．所以∠CBA=60°．
所以
| BP |
| 1 |
| 2 |
| BA |
| 1 |
| 2 |
| BC |
| BD |
| 1 |
| 2 |
| BA |
| BC |
| BD |
| 1 |
| 2 |
| CA |
| BD |
由正方体的性质可知，BD⊥CO，BD⊥AO，故BD⊥面ACO，所以AC⊥BD．
所以|
| BP |
| 1 |
| 2 |
| CA |
| BD |
| 1 |
| 2 |
| CA |
| BD |
=
| 1 |
| 4 |
| CA |
| BD |
| CA |
| BD |
=
| 1 |
| 4 |
| 9 |
| 4 |
故|
| BP |
| 3 |
| 2 |
故选A
点评：本题考查了平面向量在解决几何问题中的应用，强调基底意识与化归思想．属于中档题．
练习册系列答案
一本好题口算题卡系列答案
相关题目
