题目内容
14.随机调查高河镇某社区80个人,以研究这一社区居民在20:00--22:00时间段的休闲方式与性别的关系,得到下面的数据表:| 休闲方式 性别 | 看电视 | 看书 | 合计 |
| 男 | 10 | 50 | 60 |
| 女 | 10 | 10 | 20 |
| 合计 | 20 | 60 | 80 |
(2)从第(1)问抽取的4位居民中随机抽取2位,恰有1男1女的概率是多少;
(3)由以上数据,能否有99%的把握认为在20:00-22:00时间段的休闲方式与性别有关系.
K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d.
参考数据:
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
分析 (1)根据分层抽样的定义即可得到结论.
(2)确定所有基本事件、满足条件的基本事件,即可求恰有一男一女的概率.
(3)根据样本提供的2×2列联表,得K2≥6.635的概率约为0.01,由此能推导出有99%的把握认为在20:00-22:00时间段的休闲方式与性别有关系.
解答 (本小题满分12分)
解:(1)这80人中,男人60人,女人20人,而男女人数之比为3:1,
所以分层抽样,男、女抽出的人数分别为3人、1人. (3分)
(2)从4人中随机抽出两人共有6种等可能结果,而一男一女共有3种结果,
所以根据古典概型可得,从第(1)问抽取的4位居民中随机抽取2位,恰有1男1女的概率是 $p=\frac{1}{2}$.(7分)
(3)由独立性检验K2计算公式得,K2=$\frac{80×(10×10-10×50)^{2}}{60×20×20×60}$=$\frac{80}{9}$≈8.889>6.635,
所以由表格中参考数据知,有99%的把握认为在20:00--22:00时间段的休闲方式与性别有关系.(12分)
点评 本题主要考查分层抽样的定义以及应用,考查是否有99%的把握认为“在20:00-22:00时间段的休闲方式与性别有关系的判断与求法,是中档题.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
4.已知f(x)=ax3,g(x)=9x2+3x-1,当x∈[1,2]时,f(x)≥g(x)恒成立,则a的取值范围是( )
| A. | a≤$\frac{41}{8}$ | B. | a≤11 | C. | a≥$\frac{41}{8}$ | D. | a≥11 |
5.已知函数y=f(x)(x∈R)的图象如图所示,则不等式(x-1)f′(x)<0的解集为( )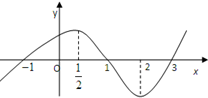

| A. | (-∞,0)∪($\frac{1}{2}$,1) | B. | (-∞,0)∪(1,2) | C. | (-∞,$\frac{1}{2}$)∪(1,2) | D. | (-∞,$\frac{1}{2}$)∪(1,+∞) |
6.若函数f(x)=$\frac{1}{3}{x^3}$-x在区间(a2-26,a)上有最大值,则实数a的取值范围为( )
| A. | (-1,5) | B. | (-1,5] | C. | (-1,2) | D. | (-1,2] |
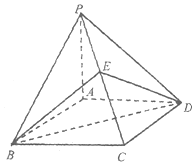 如图,已知四棱锥P-ABCD的底面ABCD是菱形,∠ABC=60°,PA⊥平面ABCD,直线PB和平面ABCD所成的角为45°,E为PC的中点.
如图,已知四棱锥P-ABCD的底面ABCD是菱形,∠ABC=60°,PA⊥平面ABCD,直线PB和平面ABCD所成的角为45°,E为PC的中点.