��Ŀ����
12��ijѧУΪ�˽�����꼶ѧ�������ڼ��ѧϰ�������ȡ�ס������࣬�������������ѧ���ں����ڼ�ÿ��ƽ��ѧϰ��ʱ�䣨��λ��Сʱ����ͳ�ƽ�����Ƶ�ʷֱ�ֱ��ͼ����ͼ������֪�ס�������ѧ��������ͬ���װ�ѧ��ÿ��ƽ��ѧϰʱ��������[2��4]����8�ˣ�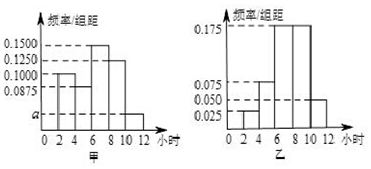
������ֱ��ͼ��a��ֵ���װ�ѧ��ÿ��ƽ��ѧϰʱ��������[10��12]��������
���Ӽס���������ÿ��ƽ��ѧϰʱ�����10��Сʱ��ѧ������ȡ4�˲μӲ��ԣ���4���мװ�ѧ��������Ϊ�Σ���εķֲ��к���ѧ������
���� ��1������Ƶ�ʷֲ�ֱ��ͼ�����ʼ��ɵó���
��2����2���Ұ�ѧϰʱ��������[10��12]������Ϊ40��0.05��2=4���ˣ����ɣ�1��֪�װ�ѧϰʱ��������[10��12]������Ϊ3�ˣ���������ѧϰʱ�����10Сʱ��ͬѧ��7�ˣ��ε����п���ȡֵΪ0��1��2��3�����ó����ηֲ��еļ��㹫ʽ������ѧ�������㹫ʽ���ɵó���
��� �⣺��1����ֱ��ͼ֪����0.150+0.125+0.100+0.0875+a����2=1�����a=0.0375��
��Ϊ�װ�ѧϰʱ��������[2��4]����8�ˣ����Լװ��ѧ������Ϊ$\frac{8}{0.2}=40$��
���Լס�������������Ϊ40�ˣ����Լװ�ѧϰʱ��������[10��12]������Ϊ40��0.0375��2=3���ˣ���
��2���Ұ�ѧϰʱ��������[10��12]������Ϊ40��0.05��2=4���ˣ���
�ɣ�1��֪�װ�ѧϰʱ��������[10��12]������Ϊ3�ˣ���������ѧϰʱ�����10Сʱ��ͬѧ��7�ˣ��ε����п���ȡֵΪ0��1��2��3.$P����=0��=\frac{C_3^0C_4^4}{C_7^4}=\frac{1}{35}$��$P����=1��=\frac{C_3^1C_4^3}{C_7^4}=\frac{12}{35}$��$P����=2��=\frac{C_3^2C_4^2}{C_7^4}=\frac{18}{35}$��$P����=3��=\frac{C_3^3C_4^1}{C_7^4}=\frac{4}{35}$��
������������εķֲ���Ϊ��
| �� | 0 | 1 | 2 | 3 |
| P | $\frac{1}{35}$ | $\frac{12}{35}$ | $\frac{18}{35}$ | $\frac{4}{35}$ |
���� ���⿼����Ƶ�ʷֲ�ֱ��ͼ�����ʡ������ηֲ��еļ��㹫ʽ������ѧ�������㹫ʽ��������������������������������е��⣮

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�| A�� | y=ln��x-2�� | B�� | y=-$\sqrt{x}$ | C�� | y=x2 | D�� | y=$\frac{1}{x}$ |
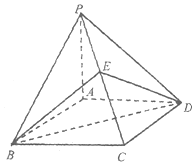 ��ͼ����֪����P-ABCD�ĵ���ABCD�����Σ���ABC=60�㣬PA��ƽ��ABCD��ֱ��PB��ƽ��ABCD���ɵĽ�Ϊ45�㣬EΪPC���е㣮
��ͼ����֪����P-ABCD�ĵ���ABCD�����Σ���ABC=60�㣬PA��ƽ��ABCD��ֱ��PB��ƽ��ABCD���ɵĽ�Ϊ45�㣬EΪPC���е㣮