题目内容
13.已知函数f(x)=|x-2|+2|x+1|.(1)解不等式f(x)>4;
(2)若关于x的不等式f(x)≥m恒成立,求实数m的取值范围.
分析 (1)通过讨论x的范围,去掉绝对值,从而解出不等式的解集;
(2)画出函数f(x)的图象,通过图象读出即可.
解答  解:(1)当x<-1时,-3x>4,解得x<-$\frac{4}{3}$,∴x<-$\frac{4}{3}$,
解:(1)当x<-1时,-3x>4,解得x<-$\frac{4}{3}$,∴x<-$\frac{4}{3}$,
当-1≤x<2时,x+4>4,解得x>0,∴0<x<2,
当x≥2时,3x>4,解得x>$\frac{4}{3}$,∴x≥2,
综上,原不等式解集为{x|x<-$\frac{4}{3}$或x>0}.
(2)由f(x)的图象和单调性易得f(x)min=f(-1)=3,
若?x∈R,f(x)≥m恒成立,
则只需f(x)min≥m⇒m≤3,
故实数m的取值范围是(-∞,3].
点评 本题考查了绝对值不等式的解法,考查函数恒成立问题,考查数形结合思想,是一道中档题.

练习册系列答案
相关题目
4.已知f(x)=ax3,g(x)=9x2+3x-1,当x∈[1,2]时,f(x)≥g(x)恒成立,则a的取值范围是( )
| A. | a≤$\frac{41}{8}$ | B. | a≤11 | C. | a≥$\frac{41}{8}$ | D. | a≥11 |
5.已知函数y=f(x)(x∈R)的图象如图所示,则不等式(x-1)f′(x)<0的解集为( )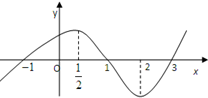

| A. | (-∞,0)∪($\frac{1}{2}$,1) | B. | (-∞,0)∪(1,2) | C. | (-∞,$\frac{1}{2}$)∪(1,2) | D. | (-∞,$\frac{1}{2}$)∪(1,+∞) |
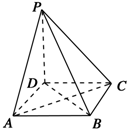 如图所示,在四棱锥P-ABCD中,底面是边长为a的正方形,侧棱PD=a,PA=PC=$\sqrt{2}$a,
如图所示,在四棱锥P-ABCD中,底面是边长为a的正方形,侧棱PD=a,PA=PC=$\sqrt{2}$a,