题目内容
15．在正项等差数列{an}中，a12=2a5-a9，且a5+a6+a7=18，则（ ）| A． | a1，a2，a3成等比数列 | B． | a2，a3，a6成等比数列 | ||
| C． | a3，a4，a8成等比数列 | D． | a4，a6，a9成等比数列 |
分析 设正项等差数列{an}的公差为d，由a12=2a5-a9，且a5+a6+a7=18，可得a12=2（a1+4d）-（a1+8d），且3a6=3（a1+5d）=18，解得a1，d，即可判断出结论．
解答 解：设正项等差数列{an}的公差为d，∵a12=2a5-a9，且a5+a6+a7=18，
则a12=2（a1+4d）-（a1+8d），且3a6=3（a1+5d）=18，
解得a1=d=1．
∴an=1+（n-1）=n．
∴a4=4，a6=6，a9=9．
∴a4，a6，a9成等比数列．
故选：D．
点评 本题考查了等差数列与等比数列的定义与通项公式，考查了推理能力与计算能力，属于中档题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
5．已知函数y=f（x）（x∈R）的图象如图所示，则不等式（x-1）f′（x）＜0的解集为（ ）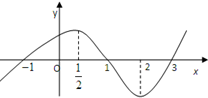
| A． | （-∞，0）∪（$\frac{1}{2}$，1） | B． | （-∞，0）∪（1，2） | C． | （-∞，$\frac{1}{2}$）∪（1，2） | D． | （-∞，$\frac{1}{2}$）∪（1，+∞） |
6．若函数f（x）=$\frac{1}{3}{x^3}$-x在区间（a2-26，a）上有最大值，则实数a的取值范围为（ ）
| A． | （-1，5） | B． | （-1，5] | C． | （-1，2） | D． | （-1，2] |
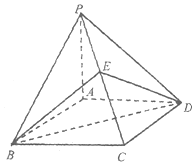如图，已知四棱锥P-ABCD的底面ABCD是菱形，∠ABC=60°，PA⊥平面ABCD，直线PB和平面ABCD所成的角为45°，E为PC的中点．