题目内容
3.已知$f(x)=\left\{\begin{array}{l}a{x^2}+x,x>0\\-x,x≤0\end{array}\right.$,若不等式f(x-1)≥f(x)对一切x∈R恒成立,则实a数的最大值为( )| A. | $-\frac{9}{16}$ | B. | -1 | C. | $-\frac{1}{2}$ | D. | 1 |
分析 作出函数f(x)的图象,利用函数f(x-1)的图象高于f(x)的图象,进行求解即可.
解答 解:作出函数f(x)和f(x-1)的图象,
当a≥0时,f(x-1)≥f(x)对一切x∈R不恒成立(如图1)
当a<0时,f(x-1)过定点(1,0)(如图2),
当x>0时,f(x)=ax2+x的两个零点为x=0和x=-$\frac{1}{a}$,
要使不等式f(x-1)≥f(x)对一切x∈R恒成立,
则只需要-$\frac{1}{a}$≤1,得a≤-1,
即a的最大值为-1,
故选:B
点评 本题主要考查不等式恒成立问题,利用函数图象平移关系,利用数形结合是解决本题的关键.综合性较强.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案
相关题目
8.为了解本市居民的生活成本,甲、乙、内三名同学利用假期分别对三个社区进行了“家庭每月日常消费额”的调查.他们将调查所得到的数据分别绘制成频率分布直方图(如图所示),甲、乙、丙所调查数据的标准差分别为x1,x2,x3,则它们的大小关系为( )
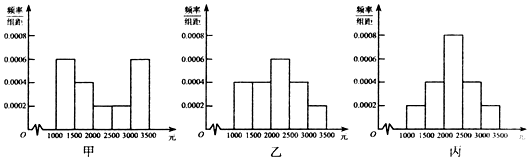

| A. | s1>s2>s3 | B. | s1>s3>s2 | C. | s3>s2>s1 | D. | s3>s1>s2 |
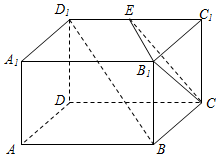 已知长方体AC1中,AD=AB=2,AA1=1,E为D1C1的中点,如图所示.
已知长方体AC1中,AD=AB=2,AA1=1,E为D1C1的中点,如图所示.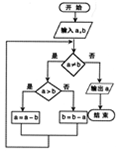 如图程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”,执行该程序框图,若输入的a,b分别为17,14,则输出的a=( )
如图程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”,执行该程序框图,若输入的a,b分别为17,14,则输出的a=( )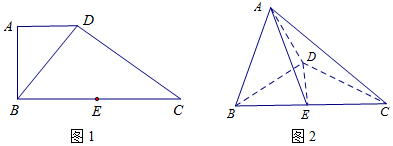
 如图,已知六棱锥P-ABCDEF的底面是正六边形,PA⊥平面ABC,PA=2AB,则下列结论正确的是④( 写出所以正确结论的序号)
如图,已知六棱锥P-ABCDEF的底面是正六边形,PA⊥平面ABC,PA=2AB,则下列结论正确的是④( 写出所以正确结论的序号)