题目内容
17．在△ABC中，已知a=8，b=5，S△ABC=12，则cos2C=$\frac{7}{25}$．分析 由已知利用三角形面积公式可求sinC的值，进而利用二倍角的余弦函数公式即可计算得解．
解答 解：在△ABC中，∵a=8，b=5，S△ABC=12=$\frac{1}{2}$absinC=$\frac{1}{2}×8×5×$sinC，
∴sinC=$\frac{3}{5}$，
∴cos2C=1-2sin2C=1-2×（$\frac{3}{5}$）2=$\frac{7}{25}$．
故答案为：$\frac{7}{25}$．
点评 本题主要考查了三角形面积公式，二倍角的余弦函数公式在解三角形中的应用，考查了转化思想，属于基础题．
练习册系列答案
学习实践园地系列答案
相关题目
7．已知函数f（x）=sin（ωx+φ）+cos（ωx+φ）（ω＞0，0＜φ＜π）是奇函数，直线y=$\sqrt{2}$与函数f（x）的图象的两个相邻交点的横坐标之差的绝对值为$\frac{π}{2}$，则（ ）
| A． | f（x）在$（0，\frac{π}{4}）$上单调递减 | B． | f（x）在$（\frac{π}{8}，\frac{3π}{8}）$上单调递减 | ||
| C． | f（x）在$（0，\frac{π}{4}）$上单调递增 | D． | f（x）在$（\frac{π}{8}，\frac{3π}{8}）$上单调递增 |
8．为了解本市居民的生活成本，甲、乙、内三名同学利用假期分别对三个社区进行了“家庭每月日常消费额”的调查．他们将调查所得到的数据分别绘制成频率分布直方图（如图所示），甲、乙、丙所调查数据的标准差分别为x1，x2，x3，则它们的大小关系为（ ）
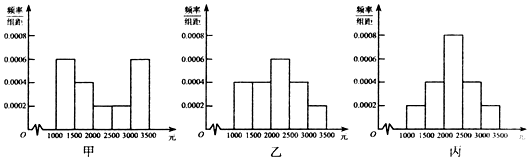
| A． | s1＞s2＞s3 | B． | s1＞s3＞s2 | C． | s3＞s2＞s1 | D． | s3＞s1＞s2 |
将石子摆成如图所示的梯形形状，称数列5，9，14，20，…为“梯形数”．根据图形的构成，此数列的第100项，即a100=5252．
2．目前，学案导学模式已经成为教学中不可或缺的一部分，为了了解学案的合理使用是否对学生的期末复习有着重要的影响，我校随机抽取100名学生，对学习成绩和学案使用程度进行了调查，统计数据如表所示：
参考公式：${K^2}=\frac{{n{{（ad-bc）}^2}}}{（a+b）（c+d）（a+c）（b+d）}$，其中n=a+b+c+d．
参考数据：
已知随机抽查这100名学生中的一名学生，抽到善于使用学案的学生概率是0.6．
（1）请将上表补充完整（不用写计算过程）；
（2）试运用独立性检验的思想方法分析：有多大的把握认为学生的学习成绩与对待学案的使用态度有关？
（3）若从学习成绩优秀的同学中随机抽取10人继续调查，采用何种方法较为合理，试说明理由．
| 善于使用学案 | 不善于使用学案 | 总计 | |
| 学习成绩优秀 | 40 | ||
| 学习成绩一般 | 30 | ||
| 总计 | 100 |
参考数据：
| P（K2≥k0） | 0.050 | 0.010 | 0.001 |
| k0 | 3.841 | 6.635 | 10.828 |
（1）请将上表补充完整（不用写计算过程）；
（2）试运用独立性检验的思想方法分析：有多大的把握认为学生的学习成绩与对待学案的使用态度有关？
（3）若从学习成绩优秀的同学中随机抽取10人继续调查，采用何种方法较为合理，试说明理由．
20．若α是第三象限角，则$\frac{α}{2}$是（ ）
| A． | 第二象限角 | B． | 第四象限角 | ||
| C． | 第二或第三象限角 | D． | 第二或第四象限角 |