题目内容
5.设函数f(x)=$\frac{1}{3}$x3-ax2+3bx-2的导函数为f′(x),若f′(x)满足f′(x+2)=f′(2-x),且f(x)≥-2在[1,3]上恒成立,则实数b的取值范围为[7,+∞).分析 先求导,根据函数的对称性,求出a的值,再分离参数,构造函数,利用导数求出函数的最大值即可
解答 解:f′(x)=3x2-2ax+2b,
∵函数f′(x)的图象关于直线x=2对称,
∴$\frac{2a}{6}$=2,即a=6.
∴f(x)=$\frac{1}{3}$x3-6x2+3bx-2
∵f(x)≥-2在[1,3]上恒成立,
即$\frac{1}{3}$x3-6x2+2bx+1≥-2在[1,3]上恒成立,
∴2b≥-$\frac{1}{3}$x2+6x-$\frac{3}{x}$在[1,3]上恒成立,
令g(x)=-$\frac{1}{3}$x2+6x-$\frac{3}{x}$,x∈[1,3],
∴g′(x)=-$\frac{2}{3}$x+6+$\frac{3}{{x}^{2}}$>0在1,3]上恒成立,
∴g(x)在[1,3]上单调递增,
∴g(x)max=g(3)=14,
∴2b≥14,
∴b≥7,
故b的范围为[7,+∞),
故答案为:[7,+∞)
点评 本题考查了利用导数研究函数的最值,利用导数研究函数的单调性,函数的单调性与导数的正负有关.本题还考查了函数的恒成立问题,一般选用参变量分离的方法进行处理,转化成求函数的最值问题.属于中档题.

练习册系列答案
相关题目
10.四名学生报名参加五项体育比赛.每人限报一项,不同的报名方法有 种( )
| A. | 45 | B. | 54 | C. | 120 | D. | 20 |
10.已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点分别为F1,F2,焦距为2$\sqrt{2}$,若直线y=-$\sqrt{3}$(x+$\sqrt{2}$)与椭圆交于点M,满足$\frac{1}{2}$∠MF1F2=∠MF2F1,则离心率是( )
| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\sqrt{3}$-1 | C. | $\frac{{\sqrt{3}-1}}{2}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
14.(x-$\frac{1}{2x}$)8的展开式中常数为( )
| A. | $\frac{1}{2}$ | B. | $\frac{35}{8}$ | C. | $\frac{3}{2}$ | D. | -$\frac{3}{2}$ |
 如图1,在边长为3的正三角形ABC中,E,F,P分别为AB,AC,BC上的点,且满足AE=FC=CP=1.将△
如图1,在边长为3的正三角形ABC中,E,F,P分别为AB,AC,BC上的点,且满足AE=FC=CP=1.将△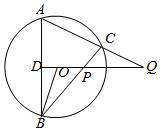 如图,A,B,C是圆O上不共线的三点,OD⊥AB于D,BC和AC分别交DO的延长线于P和Q,求证:∠OBP=∠CQP.
如图,A,B,C是圆O上不共线的三点,OD⊥AB于D,BC和AC分别交DO的延长线于P和Q,求证:∠OBP=∠CQP.