题目内容
如图,矩形ABCD中AB=2,BC=3,沿BD将矩形ABCD折叠,连结AC,所得三棱锥A-BCD的正视图和俯视图如下,则三棱锥A-BCD的侧视图的面积为
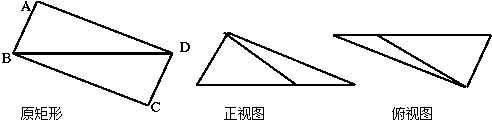

考点:简单空间图形的三视图
专题:计算题,空间位置关系与距离
分析:由题意可知平面ABD⊥平面BCD,三棱锥A-BCD侧视图为等腰直角三角形,两条直角边分别是过B和D向AC所做的垂线,做出直角边的长度,得到侧视图的面积.
解答:
 解:由正视图和俯视图可知平面ABD⊥平面BCD.
解:由正视图和俯视图可知平面ABD⊥平面BCD.
三棱锥A-BCD侧视图为等腰直角三角形,两条直角边分别是过A和C向BD所做的垂线,
由等面积可得直角边长为
=
,
∴侧视图面积为
×
×
=
.
故答案为:
.
 解:由正视图和俯视图可知平面ABD⊥平面BCD.
解:由正视图和俯视图可知平面ABD⊥平面BCD.三棱锥A-BCD侧视图为等腰直角三角形,两条直角边分别是过A和C向BD所做的垂线,
由等面积可得直角边长为
| 2×3 | ||
|
| 6 | ||
|
∴侧视图面积为
| 1 |
| 2 |
| 6 | ||
|
| 6 | ||
|
| 18 |
| 13 |
故答案为:
| 18 |
| 13 |
点评:本题考查简单几何体的三视图,根据所给的两个三视图得到直观图,这是三视图经常考查的知识点,是一个基础题.

练习册系列答案
相关题目
若复数x满足
=3-2i,则x=( )
| x |
| 1+i |
| A、1-5i | B、1+5i |
| C、5+i | D、1-i |
空间三条直线,任何两条不共面,且两两互相垂直,另一条直线l与这三条直线所成的角均为α,则tanα=( )
| A、1 | ||
B、
| ||
C、
| ||
D、2
|
已知a>0,b>0,则下列不等式中不恒成立的是( )
A、
| ||||||
B、(a+b)(
| ||||||
C、
| ||||||
| D、a2+b2+1≥2a+2b |
以下有关线性回归分析的说法不正确的是( )
A、在回归线方程
| ||||
B、用最二乘法求回归直线方程,是寻求使
| ||||
| C、相关系数为r,若r2越接近1,则表明回归线的效果越好 | ||||
| D、相关系数r越小,表明两个变量相关性越弱 |

