题目内容
半径为R的球O中有一内接圆柱.当圆柱的侧面积最大时,圆柱的侧面积与球的表面积之比是 .
考点:球的体积和表面积
专题:计算题,空间位置关系与距离
分析:设出圆柱的上底面半径为r,球的半径与上底面夹角为α,求出圆柱的侧面积表达式,求出最大值,计算球的表面积,即可得到两者的比值.
解答:
解:设圆柱的上底面半径为r,球的半径与上底面夹角为α,则r=Rcosα,圆柱的高为2Rsinα,圆柱的侧面积为:2πR2sin2α,当且仅当α=
时,sin2α=1,圆柱的侧面积最大,
圆柱的侧面积为:2πR2,球的表面积为:4πR2,
所以圆柱的侧面积与球的表面积之比是1:2.
故答案为:1:2.
| π |
| 4 |
圆柱的侧面积为:2πR2,球的表面积为:4πR2,
所以圆柱的侧面积与球的表面积之比是1:2.
故答案为:1:2.
点评:本题是基础题,考查球的内接圆柱的知识,球的表面积,圆柱的侧面积的最大值的求法,考查计算能力,常考题型.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
若M为RT△ABC斜边AB的中点,PM⊥平面ABC,则( )
| A、PA=PB=PC |
| B、PA=PB>PC |
| C、PA=PB<PC |
| D、PA≠PB |
空间三条直线,任何两条不共面,且两两互相垂直,另一条直线l与这三条直线所成的角均为α,则tanα=( )
| A、1 | ||
B、
| ||
C、
| ||
D、2
|
若某几何体的三视图如图所示,则此几何体的体积等于( )
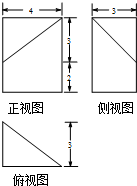

| A、4 | B、12 | C、24 | D、30 |
一个简单几何体的主视图,左视图如图所示,则其俯视图不可能为( )


| A、长方形 | B、直角三角形 |
| C、圆 | D、椭圆 |
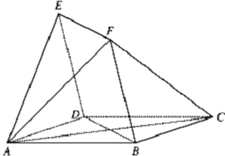 如图,四边形ABCD与BDEF 均为菱形,∠DAB=∠DBF=60°,且FA=FC.
如图,四边形ABCD与BDEF 均为菱形,∠DAB=∠DBF=60°,且FA=FC.