题目内容
设
是非零向量,λ是非零实数,下列结论中正确的是( )
| a |
A、
| ||||
B、|-λ
| ||||
C、
| ||||
D、|-λ
|
考点:向量数乘的运算及其几何意义
专题:平面向量及应用
分析:讨论λ>0或λ<0时,
与-λ
的方向问题,判断A错误;
讨论|λ|≥1或|λ|<1时,|-λ
|与|
|的大小,判断B错误;
由|-λ
|是实数,|λ|
是向量,从而判断D错误.
| a |
| a |
讨论|λ|≥1或|λ|<1时,|-λ
| a |
| a |
由|-λ
| a |
| a |
解答:
解:对于A,λ>0时,
与-λ
的方向相反,λ<0时,
与-λ
的方向相同,∴选项A错误;
对于B,|λ|≥1时,|-λ
|≥|
|,|λ|<1时,|-λ
|<|
|,∴选项B错误;
对于C,∵λ≠0,∴
与λ2
的方向相同,选项C正确;
对于D,|-λ
|是实数,|λ|
是向量,二者不相等,∴选项D错误.
故选:C.
| a |
| a |
| a |
| a |
对于B,|λ|≥1时,|-λ
| a |
| a |
| a |
| a |
对于C,∵λ≠0,∴
| a |
| a |
对于D,|-λ
| a |
| a |
故选:C.
点评:本题考查了平面向量的应用问题,解题时应对每一个选项进行讨论,以便得出正确的判断,是基础题.

练习册系列答案
相关题目
函数f(x)=-2x+ax3,若f′(2)=1,则a=( )
| A、4 | ||
B、
| ||
| C、-4 | ||
D、-
|
| sin2600° |
A、±
| ||||
B、
| ||||
C、-
| ||||
D、
|
数列{an}满足:a1a2a3…an=
,则a2013=( )
| 1 |
| n |
A、
| ||
B、
| ||
C、
| ||
D、
|
若复数m2-2m-3+(m2-3m-4)i为纯虚数(i为虚数单位),则实数m=( )
| A、m=-1 |
| B、m=3 |
| C、m=-1或 m=3 |
| D、m=0 |
若n为奇数,8n-Cn18n-1+Cn28n-2-…+Cnn-18被6除所得的余数是( )
| A、0 | B、1 | C、2 | D、3 |
判定下列命题
①第一象限的角为锐角
②f(x)=xcosx为奇函数
③
-
=
④(
•
)•
=
•(
•
)
正确的为( )
①第一象限的角为锐角
②f(x)=xcosx为奇函数
③
| AB |
| AC |
| CB |
④(
| a |
| b |
| c |
| a |
| b |
| c |
正确的为( )
| A、①② | B、①③ | C、②③ | D、①④ |
设f(x)=
x3+ax2+5x+6在区间[1,3]上单调函数,则实数a的取值范围为( )
| 1 |
| 3 |
A、[-
| ||
| B、(-∞,-3] | ||
C、[-3,
| ||
D、(-∞,-3]∪[-
|
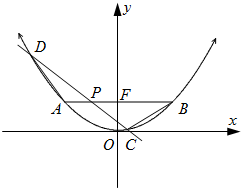 如图,已知抛物线M的参数方程为
如图,已知抛物线M的参数方程为