题目内容
1.已知定点A($\sqrt{2}$,1),动点M(x,y)的横、纵坐标同时满足三个条件:0≤x≤$\sqrt{2}$,y≤2,ax-y≤0,则$\overrightarrow{OA•}$$\overrightarrow{OM}$的最大值为4的充分不必要条件是( )| A. | a≥0 | B. | 1≤a≤$\sqrt{3}$ | C. | a≤$\sqrt{2}$ | D. | 0≤a≤$\sqrt{2}$ |
分析 先画出大值的其可行域,根据向量的数量积得到目标函数,利用线性规划的知识可以得到所以直线y=-$\sqrt{2}$x+z经过点B($\sqrt{2}$,2),即可求出a的最大值,根据充分不必要的定义即可判断答案.
解答 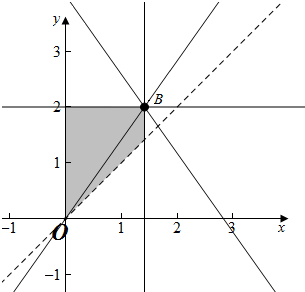 解:因为$\left\{\begin{array}{l}{0≤x≤\sqrt{2}}\\{y≤2}\\{ax+y≤0}\end{array}\right.$.其可行域为:如图所示
解:因为$\left\{\begin{array}{l}{0≤x≤\sqrt{2}}\\{y≤2}\\{ax+y≤0}\end{array}\right.$.其可行域为:如图所示
z=$\overrightarrow{OA•}$$\overrightarrow{OM}$=$\sqrt{2}$x+y,
即y=-$\sqrt{2}$x+z,作出y=-$\sqrt{2}$x+z,将此直线平行移动,因为z的最大值为4,所以直线y=-$\sqrt{2}$x+z经过点B($\sqrt{2}$,2),
所以-$\sqrt{2}$a+2≥0,
所以a≤$\sqrt{2}$,
所以则$\overrightarrow{OA•}$$\overrightarrow{OM}$的最大值为4的充分不必要条件是0≤a≤$\sqrt{2}$,
故选:D.
点评 本题主要考查线性规划的应用,充分必要条件的应用,根据向量的数量积公式是解决本题的关键.

练习册系列答案
相关题目
12.表是某市从3月份中随机抽取的10天空气质量指数(AQI)和“PM2.5”(直径小于等于2.5微米的颗粒物)24小时平均浓度的数据,空气质量指数(AQI)小于100表示空气质量优良.
(1)根据表数据,估计该市当月某日空气质量优良的概率;
(2)在表数据中、在表示空气质量优良的日期中,随机抽取两个对其当天的数据作进一步的分析,设事件M为“抽取的两个日期中,当天‘PM2.5’的24小时平均浓度小于75ug/m3”,求事件M发生的概率.
| 日期编号 | A1 | A2 | A3 | A4 | A5 | A6 | A7 | A8 | A9 | A10 |
| 空气质量指数(AQI) | 179 | 40 | 98 | 124 | 29 | 133 | 241 | 424 | 95 | 89 |
| PM2.5日均浓度(ug/m3) | 135 | 5 | 80 | 94 | 80 | 100 | 190 | 387 | 70 | 66 |
(2)在表数据中、在表示空气质量优良的日期中,随机抽取两个对其当天的数据作进一步的分析,设事件M为“抽取的两个日期中,当天‘PM2.5’的24小时平均浓度小于75ug/m3”,求事件M发生的概率.
16.函数y=Asin(ωx+φ)+b(A>0,ω>0)的部分图象如图所示,则Aω+b2等于( )
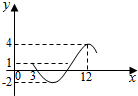

| A. | $\frac{2π+3}{3}$ | B. | $\frac{π+2}{2}$ | C. | $\frac{π+3}{3}$ | D. | π+1 |
13.已知经过点M(4,0)的直线交抛物线y2=4x于A、B两点,则以线段AB为直径的圆与原点的位置关系是( )
| A. | 原点在圆内 | B. | 原点在圆上 | C. | 原点在圆外 | D. | 不能确定 |