题目内容
11．过点A（2，-1）和B（4，5）的直线方程是3x-y-7=0．分析 根据题意，由A、B的坐标，将其代入直线的两点式方程中可得$\frac{y-5}{5-（-1）}$=$\frac{x-4}{4-2}$，将其变形可得答案．
解答 解：根据题意，点A（2，-1）、B（4，5），
则过点A（2，-1）和B（4，5）的直线方程为$\frac{y-5}{5-（-1）}$=$\frac{x-4}{4-2}$，
变形可得：3x-y-7=0，
故过点A（2，-1）和B（4，5）的直线方程是3x-y-7=0．
点评 本题考查直线方程的求法，关键是牢记直线的两点式方程．
练习册系列答案
相关题目
1．已知定点A（$\sqrt{2}$，1），动点M（x，y）的横、纵坐标同时满足三个条件：0≤x≤$\sqrt{2}$，y≤2，ax-y≤0，则$\overrightarrow{OA•}$$\overrightarrow{OM}$的最大值为4的充分不必要条件是（ ）
| A． | a≥0 | B． | 1≤a≤$\sqrt{3}$ | C． | a≤$\sqrt{2}$ | D． | 0≤a≤$\sqrt{2}$ |
19．过点（2，1）且平行于直线3x-y+2=0的直线方程为（ ）
| A． | 3x+y-7=0 | B． | 3x-y-5=0 | C． | x+3y-5=0 | D． | x-3y+1=0 |
6．在平面直角坐标系中，已知角α的终边经过点A（5，-12），则sinα=（ ）
| A． | -$\frac{12}{13}$ | B． | $\frac{5}{13}$ | C． | -$\frac{5}{12}$ | D． | -$\frac{12}{5}$ |
函数f（x）=2sin（ωx+φ）（ω＞0，-$\frac{π}{2}$＜φ＜$\frac{π}{2}$）的部分图象如图所示，x∈R．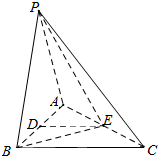
如图，在三棱锥P-ABC中，点D为AB上一点，点E为AC的中点，PA=PB=AB，BC=$\sqrt{2}$PE，∠PED=45°，DE∥平面PBC．