题目内容
16.函数y=Asin(ωx+φ)+b(A>0,ω>0)的部分图象如图所示,则Aω+b2等于( )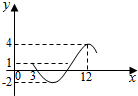
| A. | $\frac{2π+3}{3}$ | B. | $\frac{π+2}{2}$ | C. | $\frac{π+3}{3}$ | D. | π+1 |
分析 由图象可得最值,可得A和B的方程组,解方程可得A和b,由周期性可得ω,计算可得.
解答 解:由题意可得A+b=4且-A+b=-2,
解得A=3,b=1,
又可得周期T满足$\frac{3}{4}$T=(12-3),
解得T=12,即$\frac{2π}{ω}$=12,解得ω=$\frac{π}{6}$,
∴Aω+b2=3×$\frac{π}{6}$+1=$\frac{π+2}{2}$
故选:B
点评 本题考查三角函数的图象和解析式,涉及函数的周期性,属基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.若函数f(x)=ax-lnx在(2,+∞)上单调递增,则实数a的取值范围是( )
| A. | (-∞,2) | B. | (-∞,2] | C. | $[{\frac{1}{2},+∞})$ | D. | $[{\frac{1}{4},+∞})$ |
7.在正项等比数列{an}中,a2=3,a8=27,则该数列第5项a5为( )
| A. | 8 | B. | 9 | C. | 10 | D. | 11 |
1.已知定点A($\sqrt{2}$,1),动点M(x,y)的横、纵坐标同时满足三个条件:0≤x≤$\sqrt{2}$,y≤2,ax-y≤0,则$\overrightarrow{OA•}$$\overrightarrow{OM}$的最大值为4的充分不必要条件是( )
| A. | a≥0 | B. | 1≤a≤$\sqrt{3}$ | C. | a≤$\sqrt{2}$ | D. | 0≤a≤$\sqrt{2}$ |
6.在平面直角坐标系中,已知角α的终边经过点A(5,-12),则sinα=( )
| A. | -$\frac{12}{13}$ | B. | $\frac{5}{13}$ | C. | -$\frac{5}{12}$ | D. | -$\frac{12}{5}$ |