题目内容
命题p：“?x0∈R，x02+2x0+2≤0”，则命题p的否定?p是 ．
考点：命题的否定
专题：简易逻辑
分析：直接利用特称命题的否定是全称命题写出结果即可．
解答：
解：因为特称命题的否定是全称命题，所以命题p：“?x0∈R，x02+2x0+2≤0”，则命题p的否定?p是：?x∈R，x2+2x+2＞0．
故答案为：?x∈R，x2+2x+2＞0．
故答案为：?x∈R，x2+2x+2＞0．
点评：本题考查命题的否定特称命题与全称命题的否定关系，基本知识的考查．
练习册系列答案
相关题目
已知
=(1，2)，
=(2x，-3)，且
∥
，则x=（ ）
| a |
| b |
| a |
| b |
| A、-3 | ||
| B、0 | ||
| C、x=16 | ||
D、x=-
|
为了丰富学生的课余生活，增加学生的阅读面，亳州一中南校计划在综合楼建造一个室内面积为800平方米的矩形电子阅览室，在阅览室内沿左右两侧与后墙内侧各保留1m宽的通道，沿前侧内墙保留3m的空地，当矩形阅览室边长各为多少时，面积最大，最大为多少？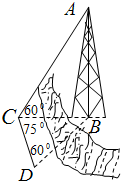
测量河对岸的塔高AB时，可以选与塔底B在同一水平面内的两个侧点C与D．现测得∠BCD=75°，∠BDC=60°，CD=100m．并在点C测得塔顶A的仰角∠ACB=60°，求：塔高AB．