题目内容
4.设全集U={1,2,3,4},集合A={x|x2-5x+4<0,x∈Z},则∁UA={1,4}.分析 求出集合A中的元素,从而求出A的补集即可.
解答 解:U={1,2,3,4},
A={x|x2-5x+4<0,x∈Z}={x|1<x<4,x∈Z}={2,3},
则∁UA={1,4},
故答案为:{1,4}.
点评 本题考查了集合的运算,考查不等式问题,是一道基础题.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
14. 已知某几何体的三视图如图所示,其中俯视图是腰长为2的等腰梯形,则该几何体的全面积为( )
已知某几何体的三视图如图所示,其中俯视图是腰长为2的等腰梯形,则该几何体的全面积为( )
 已知某几何体的三视图如图所示,其中俯视图是腰长为2的等腰梯形,则该几何体的全面积为( )
已知某几何体的三视图如图所示,其中俯视图是腰长为2的等腰梯形,则该几何体的全面积为( )| A. | $40+6\sqrt{3}$ | B. | $40+12\sqrt{3}$ | C. | 12$\sqrt{3}$ | D. | 24$\sqrt{3}$ |
16.若Sn=sin$\frac{π}{7}$+sin$\frac{2π}{7}$+…+sin$\frac{nπ}{7}$(n∈N+),则在S1,S2,…,S2017中,值为零的个数是( )
| A. | 143 | B. | 144 | C. | 287 | D. | 288 |
13.过点(1,2)且与直线y=2x+1垂直的直线的方程为( )
| A. | x+2y-3=0 | B. | 2x-y+4=0 | C. | x+2y+3=0 | D. | x+2y-5=0 |
14.在平面直角坐标系xOy中,椭圆C的中心为原点,焦点F1,F2在x轴上,离心率为$\frac{1}{2}$,点P为椭圆上一点,且△PF1F2的周长为12,那么C的方程为( )
| A. | $\frac{{x}^{2}}{25}$+y2=1 | B. | $\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{4}$=1 | C. | $\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{24}$=1 | D. | $\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{12}$=1 |




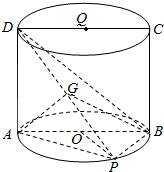 如图,四边形ABCD是体积为8$\sqrt{3}$π的圆柱OQ的轴截面,点P在底面圆周上,BP=OA=2,G是DP的中点.
如图,四边形ABCD是体积为8$\sqrt{3}$π的圆柱OQ的轴截面,点P在底面圆周上,BP=OA=2,G是DP的中点.