题目内容
14.在平面直角坐标系xOy中,椭圆C的中心为原点,焦点F1,F2在x轴上,离心率为$\frac{1}{2}$,点P为椭圆上一点,且△PF1F2的周长为12,那么C的方程为( )| A. | $\frac{{x}^{2}}{25}$+y2=1 | B. | $\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{4}$=1 | C. | $\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{24}$=1 | D. | $\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{12}$=1 |
分析 由题意可得$\left\{\begin{array}{l}{2a+2c=12}\\{\frac{c}{a}=\frac{1}{2}}\end{array}\right.$,又b2=a2-c2.联立解出即可得出椭圆C的方程.
解答 解:由题意可得$\left\{\begin{array}{l}{2a+2c=12}\\{\frac{c}{a}=\frac{1}{2}}\end{array}\right.$,又b2=a2-c2.解得a=4,c=2.
∴b2=a2-c2=12.∴椭圆C的方程为$\frac{{x}^{2}}{16}+\frac{{y}^{2}}{12}=1$.
故选:D.
点评 本题考查了椭圆的定义标准方程及其性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案
相关题目
2.“大众创业,万众创新”是李克强总理在本届政府工作报告中向全国人民发出的口号.某生产企业积极响应号召,大力研发新产品,为了对新研发的一批产品进行合理定价,将该产品按事先拟定的价格进行试销,得到一组销售数据(xi,yi)(i=1,2,…,6),如表所示:
已知$\overline y=\frac{1}{6}\sum_{i=1}^6{y_i}$=80.
(Ⅰ)求出q的值;
(Ⅱ)已知变量x,y具有线性相关关系,求产品销量y(件)关于试销单价x(元)的线性回归方程$\widehaty=\widehatbx+\widehata$;
(Ⅲ)用$\widehat{y_i}$表示用(Ⅱ)中所求的线性回归方程得到的与xi对应的产品销量的估计值.当销售数据(xi,yi)对应的残差的绝对值$|\widehat{y_i}-{y_i}|≤1$时,则将销售数据(xi,yi)称为一个“好数据”.现从6个销售数据中任取3个,求“好数据”个数ξ的分布列和数学期望E(ξ).
(参考公式:线性回归方程中$\widehatb$,$\widehata$的最小二乘估计分别为$\widehatb=\frac{{\sum_{i=1}^n{{x_i}{y_i}}-n\overline x\overline y}}{{\sum_{i=1}^n{x_i^2}-n{{\overline x}^2}}}$,$\widehata=\overline y-\widehatb\overline x$)
| 试销单价x(元) | 4 | 5 | 6 | 7 | 8 | 9 |
| 产品销量y(件) | q | 84 | 83 | 80 | 75 | 68 |
(Ⅰ)求出q的值;
(Ⅱ)已知变量x,y具有线性相关关系,求产品销量y(件)关于试销单价x(元)的线性回归方程$\widehaty=\widehatbx+\widehata$;
(Ⅲ)用$\widehat{y_i}$表示用(Ⅱ)中所求的线性回归方程得到的与xi对应的产品销量的估计值.当销售数据(xi,yi)对应的残差的绝对值$|\widehat{y_i}-{y_i}|≤1$时,则将销售数据(xi,yi)称为一个“好数据”.现从6个销售数据中任取3个,求“好数据”个数ξ的分布列和数学期望E(ξ).
(参考公式:线性回归方程中$\widehatb$,$\widehata$的最小二乘估计分别为$\widehatb=\frac{{\sum_{i=1}^n{{x_i}{y_i}}-n\overline x\overline y}}{{\sum_{i=1}^n{x_i^2}-n{{\overline x}^2}}}$,$\widehata=\overline y-\widehatb\overline x$)
9.设函数f'(x)是定义在(0,π)上的函数f(x)的导函数,有f(x)sinx-f'(x)cosx<0,$a=\frac{1}{2}f(\frac{π}{3})$,b=0,$c=-\frac{{\sqrt{3}}}{2}f(\frac{5π}{6})$,则( )
| A. | a<b<c | B. | b<c<a | C. | c<b<a | D. | c<a<b |
19.“x2+5x-6>0”是“x>2”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
6.计算:log5100+log50.25的值是( )
| A. | 0 | B. | 1 | C. | 2 | D. | 4 |
3.已知函数f(x)满足f($\frac{1}{x}$)+$\frac{1}{x}$f(-x)=2x(x≠0),则f(-2)=( )
| A. | $-\frac{7}{2}$ | B. | $\frac{9}{2}$ | C. | $\frac{7}{2}$ | D. | $-\frac{9}{2}$ |
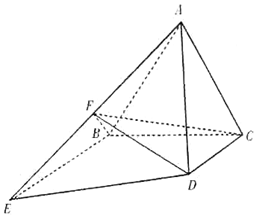 如图所示,正三角形ABC所在平面与梯形BCDE所在平面垂直,BE∥CD,BE=2CD=4,BE⊥BC,F为棱AB的中点.
如图所示,正三角形ABC所在平面与梯形BCDE所在平面垂直,BE∥CD,BE=2CD=4,BE⊥BC,F为棱AB的中点.