题目内容
14. 已知某几何体的三视图如图所示,其中俯视图是腰长为2的等腰梯形,则该几何体的全面积为( )
已知某几何体的三视图如图所示,其中俯视图是腰长为2的等腰梯形,则该几何体的全面积为( )| A. | $40+6\sqrt{3}$ | B. | $40+12\sqrt{3}$ | C. | 12$\sqrt{3}$ | D. | 24$\sqrt{3}$ |
分析 根据三视图画出其直观图,利用三视图的数据求出底面等腰梯形的面积,代棱柱的体积公式计算即可.
解答 解:由三视图判断几何体为直四棱柱,其直观图如图:
其底面为等腰梯形,由侧视图知梯形的高为$\sqrt{3}$,由正视图知棱柱的高为4,
侧面积s1=(4+2+2+2)×4=40,底面积s2=(4+2)×$\sqrt{3}$×$\frac{1}{2}$=3$\sqrt{3}$.
该几何体的全面积为40+6$\sqrt{3}$.
故选:A.
点评 本题考查的知识点是由三视图求表面积积,其中根据已知的三视图分析出几何体的形状是解答的关键.属于中档题

练习册系列答案
相关题目
20.已知复数z满足$\frac{z}{|z|}=\frac{3}{5}+\frac{4}{5}i$,则z的实部与虚部之比为( )
| A. | $\frac{3}{4}$ | B. | $\frac{4}{3}$ | C. | $-\frac{4}{3}$ | D. | $-\frac{3}{4}$ |
9.直线3x+4y-2=0和直线6x+8y+1=0的距离是( )
| A. | $\frac{3}{5}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{10}$ | D. | $\frac{1}{5}$ |
3.某几何体的三视图中的三角形都是直角三角形.如图所示.则该几何体中直角三角形的个数为( )


| A. | 1 | B. | 2 | C. | 3 | D. | 4 |

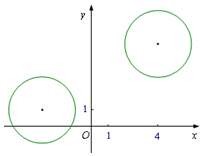 在平面直角坐标系xOy中,已知圆${C_1}:{(x+3)^2}+{(y-1)^2}=4$和圆${C_2}:{(x-4)^2}+{(y-5)^2}=4$.
在平面直角坐标系xOy中,已知圆${C_1}:{(x+3)^2}+{(y-1)^2}=4$和圆${C_2}:{(x-4)^2}+{(y-5)^2}=4$.