题目内容
1.函数y=$\frac{lg(1-tanx)}{\sqrt{1-2sinx}}$的定义域是{x|$-\frac{π}{2}+2kπ<x<\frac{π}{6}+2kπ$或$\frac{5π}{6}+2kπ<x<\frac{5π}{4}+2kπ,k∈Z$}.分析 由对数式的真数大于0,分母中根式内部的代数式大于0联立不等式组求解.
解答 解:要使原函数有意义,则$\left\{\begin{array}{l}{1-tanx>0①}\\{1-2sinx>0②}\end{array}\right.$,
解①得:$-\frac{π}{2}+kπ<x<\frac{π}{4}+kπ,k∈Z$;
解②得:$-\frac{7π}{6}+2kπ<x<\frac{π}{6}+2kπ,k∈Z$.
取交集得:$-\frac{π}{2}+2kπ<x<\frac{π}{6}+2kπ$或$\frac{5π}{6}+2kπ<x<\frac{5π}{4}+2kπ,k∈Z$.
∴函数y=$\frac{lg(1-tanx)}{\sqrt{1-2sinx}}$的定义域是{x|$-\frac{π}{2}+2kπ<x<\frac{π}{6}+2kπ$或$\frac{5π}{6}+2kπ<x<\frac{5π}{4}+2kπ,k∈Z$}.
故答案为:{x|$-\frac{π}{2}+2kπ<x<\frac{π}{6}+2kπ$或$\frac{5π}{6}+2kπ<x<\frac{5π}{4}+2kπ,k∈Z$}.
点评 本题考查函数的定义域及其求法,训练了三角不等式的解法,是基础题.

练习册系列答案
相关题目
16.下列各式的大小关系正确的是( )
| A. | sin11°>sin168° | B. | sin194°<cos160° | ||
| C. | tan(-$\frac{π}{5}$)<tan(-$\frac{3π}{7}$) | D. | cos(-$\frac{15π}{8}$)>cos$\frac{14π}{9}$ |
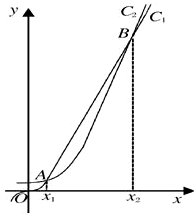 函数f(x)=2x和g(x)=x3的部分图象的示意图如图所示.设两函数的图象交于点A(x1,y1)、B(x2,y2),x1<x2.
函数f(x)=2x和g(x)=x3的部分图象的示意图如图所示.设两函数的图象交于点A(x1,y1)、B(x2,y2),x1<x2.