题目内容
14.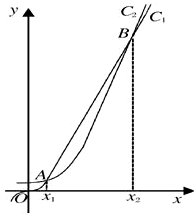 函数f(x)=2x和g(x)=x3的部分图象的示意图如图所示.设两函数的图象交于点A(x1,y1)、B(x2,y2),x1<x2.
函数f(x)=2x和g(x)=x3的部分图象的示意图如图所示.设两函数的图象交于点A(x1,y1)、B(x2,y2),x1<x2.(1)请指出示意图中曲线C1、C2分别对应哪一个函数?
(2)若x1∈[a,a+1],x2∈[b,b+1],且a,b∈{1,2,3,4,5,6,7,8,9,10,11,12},指出a、b的值,并说明理由;
(3)结合函数图象示意图,判断f(6)、g(6)、f(2010)、g(2010)的大小.
分析 (1)根据函数f(x)=2x的图象过点(0,1),g(x)=x3的图象过点(0,0)判断即可;
(2)结合函数的零点的判定定理判断即可;
(3)结合图象可知,f(6)<g(6)<g(2010)<f(2010).
解答 解:(1)∵函数f(x)=2x的图象过点(0,1),∴C2是其图象;
∵g(x)=x3的图象过点(0,0),∴C1是其图象;
(2)∵f(1)>g(1),f(2)<g(2),
∴x1∈[1,2],故a=1;
∵f(9)<g(9),f(10)>g(10)
∴x2∈[9,10],故b=9;
(3)结合图象可知,
f(6)<g(6)<g(2010)<f(2010).
点评 本题考查了指数函数与幂函数的性质,同时考查了数形结合的思想应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
5.数列{an}为等比数列,Sn是数列{an}的前n项和,且Sn>0,a6是a5、a4的等差中项,则数列{an}的公比q为( )
| A. | -$\frac{1}{2}$或1 | B. | $\frac{1}{2}$或1 | C. | 1 | D. | -$\frac{1}{2}$ |
19.已知c>0,设命题p:函数y=cx为减函数.命题q:当$x∈[{\frac{1}{2},2}]$时,函数f(x)=x+$\frac{1}{x}>\frac{1}{c}$恒成立.如果p或q为真命题,p且q为假命题,求c的取值范围( )
| A. | $({0,\frac{1}{2}})$ | B. | $[{\frac{1}{2},1}]$ | C. | $({0,\frac{1}{2}}]∪[{1,+∞})$ | D. | (2,+∞) |