题目内容
10.在直角梯形ABCD中,已知BC∥AD,AB⊥AD,AB=AD=4,BC=2,若P为线段CD上一点,且满足$\overrightarrow{DP}=λ\overrightarrow{DC}$,$\overrightarrow{PA}$•$\overrightarrow{PB}$=5,则$|{\overrightarrow{PA}}$|=$\sqrt{13}$.分析 由题意和向量的线性运算求出$\overrightarrow{CD}$,$\overrightarrow{DP}$,$\overrightarrow{PC}$,再求出$\overrightarrow{PC}$和$\overrightarrow{PB}$,代入$\overrightarrow{PA}•\overrightarrow{PB}$,利用向量的数量积运算化简即可.
解答 解:由题意可得,BC∥AD、BC=2,AD=4,则$\overrightarrow{AD}=2\overrightarrow{BC}$,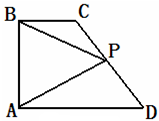
所以$\overrightarrow{CD}=\overrightarrow{CB}+\overrightarrow{BA}+\overrightarrow{AD}$=$\overrightarrow{BA}+\overrightarrow{BC}$,
因为P为CD的中点,所以$\overrightarrow{DP}$=$λ\overrightarrow{DC}$=-λ($\overrightarrow{BA}+\overrightarrow{BC}$),
因为$\overrightarrow{PA}$=$\overrightarrow{PD}$$+\overrightarrow{DA}$=$\overrightarrow{PD}$-2$\overrightarrow{BC}$,$\overrightarrow{PB}$=$\overrightarrow{PC}+\overrightarrow{CB}$,则$\overrightarrow{PA}•\overrightarrow{PB}$=($\overrightarrow{PD}-2\overrightarrow{BC}$)•($\overrightarrow{PC}$+$\overrightarrow{CB}$)=(λ$\overrightarrow{BA}$+$λ\overrightarrow{BC}$-2$\overrightarrow{BC}$)[(1-λ)λ($\overrightarrow{CB}+\overrightarrow{AB}$)]=5,又$\overrightarrow{AB}•\overrightarrow{BC}$=0,且AB=4,BC=2,
所以λ=$\frac{1}{2}$;
所以$\overrightarrow{PA}$=$\overrightarrow{PD}$$+\overrightarrow{DA}$=$\overrightarrow{PD}$-2$\overrightarrow{BC}$,
$|{\overrightarrow{PA}}$|=$\sqrt{P{D}^{2}+4B{C}^{2}-4\overrightarrow{PD}•\overrightarrow{BC}}$=$\sqrt{13}$;
故答案为:$\sqrt{13}$.
点评 本题考查了平面向量的加减运算、数量积运算以及模的求法;属于中档题.

 阅读快车系列答案
阅读快车系列答案| A. | -$\frac{1}{2}$或1 | B. | $\frac{1}{2}$或1 | C. | 1 | D. | -$\frac{1}{2}$ |
| A. | 2 | B. | $\frac{5}{2}$ | C. | 3 | D. | 4 |
| A. | $({0,\frac{1}{2}})$ | B. | $[{\frac{1}{2},1}]$ | C. | $({0,\frac{1}{2}}]∪[{1,+∞})$ | D. | (2,+∞) |
| A. | a<5 | B. | |a|<4 | C. | a2<25 | D. | -5<a<5 |