题目内容
已知双曲线C的方程为
-
=1（a＞0，b＞0），它的左、右焦点分别F1，F2，左右顶点为A1，A2，过焦点F2先作其渐近线的垂线，垂足为P，再作与x轴垂直的直线与曲线C交于点Q，R，若|PF2|，|A1A2|，|QF1|依次成等差数列，则离心率e=（ ）
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点：双曲线的简单性质
专题：计算题,等差数列与等比数列,直线与圆,圆锥曲线的定义、性质与方程
分析：由题设条件推导出|F2P|=b，|QF1|=2a+
，|A1A2|=2a，由|PF2|，|A1A2|，|QF1|依次成等差数列，知b，2a，2a+
依次成等差数列，由此能求出离心率e．
| b2 |
| a |
| b2 |
| a |
解答：
解：由题设知双曲线C：
-
=1
的一条渐近线方程为
l：y=
x，
∵右焦点F（c，0），∴F2P⊥l，
∴|F2P|=
=
=b，
∵F2Q⊥x轴，
-
=1，解得|F2Q|=
，
∴|QF1|=2a+
，
∵|A1A2|=2a，若|PF2|，|A1A2|，|QF1|依次成等差数列，
∴b，2a，2a+
依次成等差数列，
∴4a=b+2a+
，
∴2=
+
，即
+e2=3，
解得e=
．
故选A．
| x2 |
| a2 |
| y2 |
| b2 |
的一条渐近线方程为l：y=
| b |
| a |
∵右焦点F（c，0），∴F2P⊥l，
∴|F2P|=
| |bc-0| | ||
|
| |bc-0| |
| c |
∵F2Q⊥x轴，
| c2 |
| a2 |
| |F2Q|2 |
| b2 |
| b2 |
| a |
∴|QF1|=2a+
| b2 |
| a |
∵|A1A2|=2a，若|PF2|，|A1A2|，|QF1|依次成等差数列，
∴b，2a，2a+
| b2 |
| a |
∴4a=b+2a+
| b2 |
| a |
∴2=
| ||
| a |
| c2-a2 |
| a2 |
| e2-1 |
解得e=
| 2 |
故选A．
点评：本题考查双曲线的离心率的求法，解题时要认真审题，注意点到直线的距离公式的灵活运用．
练习册系列答案
相关题目
如图，等腰梯形ABCD中，AB∥CD且AB=2，AD=1，DC=2x（x∈（0，1））．以A，B为焦点，且过点D的双曲线的离心率为e1；以C，D为焦点，且过点A的椭圆的离心率为e2，则e1+e2的取值范围为下列命题正确的是（ ）
| A、平行于同一平面的两条直线一定平行 |
| B、夹在两平行平面间的等长线段必平行 |
| C、若平面外的直线a与平面α内的一条直线平行，则a∥平面α |
| D、如果一平面内的无数条直线平行于另一个平面，那么这两个平面平行 |
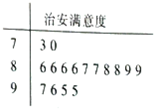某网站用“10分制”调查一社区人们的治安满意度，现从调查人群中随机抽取16名，以下茎叶图记录了他们的治安满意度分数（以小数点前的一位数字为茎，小数点后的一位数字为叶）：