题目内容
已知函数f(x)=ex-ax-1(a∈R),其中e为自然对数的底数.
(Ⅰ)若f(x)≥0对任意x≥0恒成立,求a的取值范围;
(Ⅱ)求证:当n≥2,n∈N时,恒有1n+4n+7n+…+(3n-2)n<
(3n)n.
(Ⅰ)若f(x)≥0对任意x≥0恒成立,求a的取值范围;
(Ⅱ)求证:当n≥2,n∈N时,恒有1n+4n+7n+…+(3n-2)n<
e
| ||
| e-1 |
考点:导数在最大值、最小值问题中的应用
专题:综合题,导数的综合应用
分析:(Ⅰ)f'(x)=ex-a.分两种情况进行讨论:①当a≤1时,易知f(x)在(0,+∞)上单调递增,可判断结论是否成立;当a>1时,利用导数求得函数的最小值,令其大于等于0,再通过构造函数可求a的范围;
(Ⅱ)由(Ⅰ)知当a=1时,ex≥x+1对任意x∈R恒成立.取x=-
(i=1,2,…,n),有1-
≤e-
,即(1-
)n≤(e-
)n≤e(
)n=e-
.各式相加整理可得结论;
(Ⅱ)由(Ⅰ)知当a=1时,ex≥x+1对任意x∈R恒成立.取x=-
| 3i-1 |
| 3n |
| 3i-1 |
| 3n |
| 3i-1 |
| 3n |
| 3i-1 |
| 3n |
| 3i-1 |
| 3n |
| 3i-1 |
| 3n |
| 3i-1 |
| 3 |
解答:
解:(Ⅰ)f'(x)=ex-a.
①当a≤1时,f'(x)=ex-a≥0对?x≥0恒成立,即f(x)在(0,+∞)上为单调递增函数;
又f(0)=0,∴f(x)≥f(0)=0对?x≥0恒成立.
②当a>1时,令f'(x)=0,得x=lna>0.
当x∈(0,lna) 时,f'(x)<0,f(x)单调递减;当x∈(lna,+∞) 时,f'(x)>0,f(x)单调递增.
若f(x)≥0对任意x≥0恒成立,则只需f(x)min=f(lna)=elna-alna-1=a-alna-1≥0,
令g(a)=a-alna-1(a>1),则g'(a)=1-lna-1=-lna<0,即g(a)在区间(1,+∞)上单调递减;
又g(1)=0.故g(a)<0在区间(1,+∞)上恒成立.即a>1时,满足a-alna-1≥0的a不存在.
综上:a≤1;
(Ⅱ)由(Ⅰ)知当a=1时,f(x)=ex-x-1,f'(x)=ex-1,易得f(x)min=f(0)=0,即ex≥x+1对任意x∈R恒成立.
取x=-
(i=1,2,…,n),有1-
≤e-
,即(1-
)n≤(e-
)n≤e(
)n=e-
.
相加即得:(1-
)n+(1-
)n+…+(1-
)n≤e-
+e-
+…+e-
.
∴(1-
)n+(1-
)n+…+(1-
)n=(
)n+(
)n+…+(
)n≤e-
+e-
+…+e-
.
故(3n-2)n+(3n-5)n+…+1n≤[e-
+e-
+…+e-
](3n)n=e-
(3n)n<
(3n)n,
故n≥2,n∈N时,恒有1n+4n+7n+…+(3n-2)n<
(3n)n.
①当a≤1时,f'(x)=ex-a≥0对?x≥0恒成立,即f(x)在(0,+∞)上为单调递增函数;
又f(0)=0,∴f(x)≥f(0)=0对?x≥0恒成立.
②当a>1时,令f'(x)=0,得x=lna>0.
当x∈(0,lna) 时,f'(x)<0,f(x)单调递减;当x∈(lna,+∞) 时,f'(x)>0,f(x)单调递增.
若f(x)≥0对任意x≥0恒成立,则只需f(x)min=f(lna)=elna-alna-1=a-alna-1≥0,
令g(a)=a-alna-1(a>1),则g'(a)=1-lna-1=-lna<0,即g(a)在区间(1,+∞)上单调递减;
又g(1)=0.故g(a)<0在区间(1,+∞)上恒成立.即a>1时,满足a-alna-1≥0的a不存在.
综上:a≤1;
(Ⅱ)由(Ⅰ)知当a=1时,f(x)=ex-x-1,f'(x)=ex-1,易得f(x)min=f(0)=0,即ex≥x+1对任意x∈R恒成立.
取x=-
| 3i-1 |
| 3n |
| 3i-1 |
| 3n |
| 3i-1 |
| 3n |
| 3i-1 |
| 3n |
| 3i-1 |
| 3n |
| 3i-1 |
| 3n |
| 3i-1 |
| 3 |
相加即得:(1-
| 2 |
| 3n |
| 5 |
| 3n |
| 3n-1 |
| 3n |
| 2 |
| 3 |
| 5 |
| 3 |
| 3n-1 |
| 3 |
∴(1-
| 2 |
| 3n |
| 5 |
| 3n |
| 3n-1 |
| 3n |
| 3n-2 |
| 3n |
| 3n-5 |
| 3n |
| 1 |
| 3n |
| 2 |
| 3 |
| 5 |
| 3 |
| 3n-1 |
| 3 |
故(3n-2)n+(3n-5)n+…+1n≤[e-
| 2 |
| 3 |
| 5 |
| 3 |
| 3n-1 |
| 3 |
| 2 |
| 3 |
1-
| ||
1-
|
e
| ||
| e-1 |
故n≥2,n∈N时,恒有1n+4n+7n+…+(3n-2)n<
e
| ||
| e-1 |
点评:本题考查利用导数研究函数的最值、证明不等式,考查恒成立问题,考查转化思想、分类讨论思想,恒成立问题常化为函数最值解决,关于不等式证明问题则对能力要求较高,注意往往用前面的结论.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
已知变量x,y满足约束条件
,则x+y的最大值是( )
|
A、
| ||
| B、2 | ||
| C、3 | ||
| D、4 |
z=x-y在
的线性约束条件下,取得最大值的可行解为( )
|
| A、(0,1) | ||||
| B、(-1,-1) | ||||
| C、(1,0) | ||||
D、(
|
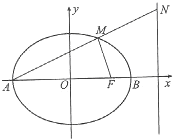 如图,已知椭圆E的中心为O,长轴的两个端点为A,B,右焦点为F,且
如图,已知椭圆E的中心为O,长轴的两个端点为A,B,右焦点为F,且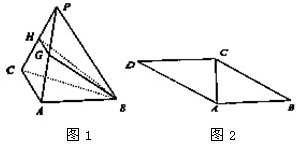 已知平行四边形ABCD (如图1)中,AB=4,BC=5,对角线AC=3,将三角形△ACD沿AC折起至△PAC位置(图2),使二面角P-AC-B为60°,G,H分别是PA,PC的中点.
已知平行四边形ABCD (如图1)中,AB=4,BC=5,对角线AC=3,将三角形△ACD沿AC折起至△PAC位置(图2),使二面角P-AC-B为60°,G,H分别是PA,PC的中点.