题目内容

3．设数列{an}的前n项和为Sn，若Sn+1=2an+1，n∈N*，则a3=（　　）
A．3B．2C．1D．0

分析 Sn+1=2an+1，n∈N*，则n=2时，可得：a2=a1+1．n=2时，a1+a2+a3=2a2+1，可得：a3．

解答 解：Sn+1=2an+1，n∈N*，则n=2时，a1+a2=2a1+1，可得：a2=a1+1．
n=2时，a1+a2+a3=2a2+1，可得：a3=2×1+1=3．
故选：A．

点评 本题考查了数列递推关系、通项公式，考查了推理能力与计算能力，属于中档题．

练习册系列答案
相关题目
13．湖面上漂着一个小球，湖水结冰后将球取出，冰面上留下了一个半径为4cm，深2cm的空穴，则该球表面积为（　　） cm2．
A．400πB．300πC．200πD．100π
14．有三张卡片，分别写有1和2，1和3，2和3，甲乙丙三人各取走一张卡片，甲看了乙的卡片后说：“我与乙的卡片上相同的数字不是2”，乙看了丙的卡片后说：“我与丙的卡片上相同的数字不是1”，丙说：“我的卡片上的数字之和不是5”，则甲的卡片上没有的数字是（　　）
A．不确定B．3C．2D．1
11．已知椭圆$C：\frac{x^2}{a^2}+{y^2}=1（a＞1）$，离心率$e=\frac{{\sqrt{6}}}{3}$．直线l：x=my+1与x轴交于点A，与椭圆C相交于E，F两点．自点E，F分别向直线x=3作垂线，垂足分别为E1，F1．
（Ⅰ）求椭圆C的方程及焦点坐标；
（Ⅱ）记△AEE1，△AE1F1，△AFF1的面积分别为S1，S2，S3，试证明$\frac{{{S_1}{S_3}}}{{{S_2}^2}}$为定值．
18．函数y=3x的值域为（　　）
A．（0，+∞）B．[1，+∞）C．（0，1]D．（0，3]
8．已知直线2x+y+2+λ（2-y）=0与两坐标轴围成一个三角形，该三角形的面积记为S（λ），当λ∈（1，+∞）时，S（λ）的最小值是（　　）
A．12B．10C．8D．6

设向量，，函数．求函数的最小正周期与最大值．

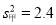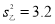甲、乙两人在相同的条件下各射靶10次，他们的环数的方差分别为：， ，则射击稳定程度是

A．甲高 B．乙高 C．两人一样高 D．不能确定
18．已知一圆台的母线长为13cm，在这个圆台中有一个半径为6cm的内切球，求这个圆台的体积．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网