题目内容
数列{an}各项均不为0,前n项和为Sn,bn=an3,bn的前n项和为Tn,且Tn=Sn2
(1)若数列{an}共3项,求所有满足要求的数列;
(2)求证:an=n(n∈N*)是满足已知条件的一个数列;
(3)请构造出一个满足已知条件的无穷数列{an},并使得a2015=-2014.
(1)若数列{an}共3项,求所有满足要求的数列;
(2)求证:an=n(n∈N*)是满足已知条件的一个数列;
(3)请构造出一个满足已知条件的无穷数列{an},并使得a2015=-2014.
考点:数学归纳法,数列的求和
专题:等差数列与等比数列
分析:(1)n=1时,T1=S12,a13=a12;n=2时,T2=S22,a13+a23=(a1+a2)2;n=3时,T3=S32,a13+a23+a33=(a1+a2+a3)2.由此能求出符合要求的数列.
(2)an=n,即证明13+23+33+…+n3=(1+2+3+…+n)2,用数学归纳法能证明an=n(n∈N*)是满足已知条件的一个数列.
(3)由已知得2an+1Sn+an+12=an+13,从而2Sn=an+12-an+1,进而得到(an+1+an)(an+1-an-1)=0=0,由此能求出结果.
(2)an=n,即证明13+23+33+…+n3=(1+2+3+…+n)2,用数学归纳法能证明an=n(n∈N*)是满足已知条件的一个数列.
(3)由已知得2an+1Sn+an+12=an+13,从而2Sn=an+12-an+1,进而得到(an+1+an)(an+1-an-1)=0=0,由此能求出结果.
解答:
(1)解:n=1时,T1=S12,a13=a12,解得a1=1或a1=0(舍),
n=2时,T2=S22,a13+a23=(a1+a2)2,
1+a23=(1+a2)2,
解得a2=2或a2=-1,或a2=0,舍,
n=3时,T3=S32,a13+a23+a33=(a1+a2+a3)2,
当a2=2时,1+8+a33=(1+2+a3)2,
解得a3=3或a3=-2,或a3=0(舍),
当a2=-1时,1-1+a33=(1-1+a3)2,
解得a3=1或a3=0(舍).
∴符合要求的数列有:1,2,3;1,2,-2;1,-1,1.
(2)证明:∵an=n,即证明13+23+33+…+n3=(1+2+3+…+n)2,
用数学归纳法证明:
①n=1时,13=12,成立.
②假设n=k时,成立,即13+23+33+…+k3=(1+2+3+…+k)2成立,
则n=k+1时,13+23+33+…+k3+(k+1)3
=(1+2+3+…+k)2+(k+1)3
=[
]2+(k+1)3
=[
]2(k2+4k+4)
=[
]2
=[
]2
=[1+2+3+…+k+(k+1)]2,也成立,
由①②,对于n∈N*,都有13+23+33+…+n3=(1+2+3+…+n)2,
∴an=n(n∈N*)是满足已知条件的一个数列.
(3)解:∵Sn2=a13+a23+a33+…+an3,①
∴Sn+12=a13+a23+…+an3+an+13,②
②-①,得2an+1Sn+an+12=an+13,
∵an+1≠0,∴2Sn+an+1=an+12,
∴2Sn=an+12-an+1,③
n≥2时,2Sn-1=an2-an,④
③-④,得2an=an+12-an+1-an2+an,
∴an+1+an=an+12-an2,
∴(an+1+an)(an+1-an-1)=0=0,
∴an+1=-an或an+1=an+1,n≥2.
构造:an=
.
n=2时,T2=S22,a13+a23=(a1+a2)2,
1+a23=(1+a2)2,
解得a2=2或a2=-1,或a2=0,舍,
n=3时,T3=S32,a13+a23+a33=(a1+a2+a3)2,
当a2=2时,1+8+a33=(1+2+a3)2,
解得a3=3或a3=-2,或a3=0(舍),
当a2=-1时,1-1+a33=(1-1+a3)2,
解得a3=1或a3=0(舍).
∴符合要求的数列有:1,2,3;1,2,-2;1,-1,1.
(2)证明:∵an=n,即证明13+23+33+…+n3=(1+2+3+…+n)2,
用数学归纳法证明:
①n=1时,13=12,成立.
②假设n=k时,成立,即13+23+33+…+k3=(1+2+3+…+k)2成立,
则n=k+1时,13+23+33+…+k3+(k+1)3
=(1+2+3+…+k)2+(k+1)3
=[
| (1+k)k |
| 2 |
=[
| (1+k) |
| 2 |
=[
| (1+k)(k+2)2 |
| 2 |
=[
| (1+k+1)(k+1) |
| 2 |
=[1+2+3+…+k+(k+1)]2,也成立,
由①②,对于n∈N*,都有13+23+33+…+n3=(1+2+3+…+n)2,
∴an=n(n∈N*)是满足已知条件的一个数列.
(3)解:∵Sn2=a13+a23+a33+…+an3,①
∴Sn+12=a13+a23+…+an3+an+13,②
②-①,得2an+1Sn+an+12=an+13,
∵an+1≠0,∴2Sn+an+1=an+12,
∴2Sn=an+12-an+1,③
n≥2时,2Sn-1=an2-an,④
③-④,得2an=an+12-an+1-an2+an,
∴an+1+an=an+12-an2,
∴(an+1+an)(an+1-an-1)=0=0,
∴an+1=-an或an+1=an+1,n≥2.
构造:an=
|
点评:本题考查所有满足要求的数列的求法,考查an=n(n∈N*)是满足已知条件的一个数列的证明,考查一个满足已知条件的无穷数列{an},并使得a2015=-2014的数列的求法,解题时要认真审题,注意数学归纳法的合理运用.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
为了得到函数y=cos(2x-
)的图象,可以将y=sin2x的图象( )
| π |
| 6 |
A、向左平移
| ||
B、向左平移
| ||
C、向右平移
| ||
D、向右平移
|
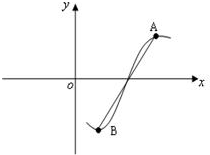 函数f(x)=cos(ωx+φ)(ω>0,0<φ<π)为R上的奇函数,该函数的部分图象如图所表示,A,B分别为最高点与最低点,并且两点间的距离为2
函数f(x)=cos(ωx+φ)(ω>0,0<φ<π)为R上的奇函数,该函数的部分图象如图所表示,A,B分别为最高点与最低点,并且两点间的距离为2