题目内容
在区域
中随机取一点P（a，b），则满足b≥sina+1的概率为 ．
|
考点：定积分,几何概型
专题：概率与统计
分析：本题是几何概型的考查，画出图形，利用几何概型概率公式，首先分别求出矩形的面积以及阴影部分的面积，然后求值．
解答：
解：如图，
由题意，满足几何概型，矩形的面积为2π×4=8π，
满足b≥sina+1的是图中阴影部分，其面积为
(4-sina-1)da=（3a+cosa）|
=6π，
所以由几何概型的概率公式得满足b≥sina+1的概率为
=
；
故答案为：
由题意，满足几何概型，矩形的面积为2π×4=8π，
满足b≥sina+1的是图中阴影部分，其面积为
| ∫ | 2π 0 |
2π 0 |
所以由几何概型的概率公式得满足b≥sina+1的概率为
| 6π |
| 4×2π |
| 3 |
| 4 |
故答案为：
| 3 |
| 4 |
点评：本题考查了几何概型的概率求法；关键是利用定积分求出满足条件的曲边梯形的面积，然后由概率公式解答．
练习册系列答案
海淀课时新作业金榜卷系列答案
期末金牌卷系列答案
轻松课堂标准练系列答案
相关题目
如图1是牡一中高二学年每天购买烤肠数量的茎叶图，第1天到第14天的购买数量依次记为A1，A2，…，A14．图2是统计茎叶图中烤肠数量在一定范围内购买次数的一个算法流程图，那么算法流程图输出的结果是（ ）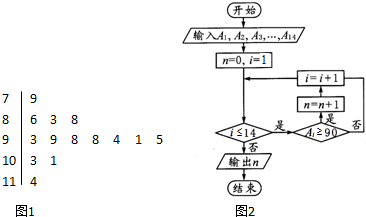
| A、7 | B、8 | C、9 | D、10 |
斜率为l且原点到直线距离为
的直线方程为（ ）
| 2 |
| A、x+y+2=0或x+y-2=0 | ||||
B、x+y+
| ||||
| C、x-y+2=0或x-y-2=0 | ||||
D、x-y+
|