题目内容
已知函数f(x)为定义在R上的奇函数,且当x>0时,f(x)=log3x,
(1)求f(x)的解析式;
(2)解不等式f(x)≤2.
(1)求f(x)的解析式;
(2)解不等式f(x)≤2.
考点:函数奇偶性的性质,函数解析式的求解及常用方法
专题:函数的性质及应用
分析:(1)根据函数为奇函数,可设x<0,则-x>0,然后将-x代入x>0时的解析式化简即可;
(2)按照分段函数分段处理的原则列出不等式,分别解之,最终取并集即可.
(2)按照分段函数分段处理的原则列出不等式,分别解之,最终取并集即可.
解答:
解:(1)易知f(0)=0;
当x<0时,则-x>0,所以f(x)=-f(-x)=-log3(-x);
所以f(x)=
.
(2)由题意:当x>0时有log3x≤2,解得0<x≤9;
当x=0时,f(0)=0显然满足题意;
当x<0时有-log3(-x)≤2,即log3(-x)≥-2,解得x≤-
.
综上可得原不等式的解集为[0,9]∪(-∞,-
].
当x<0时,则-x>0,所以f(x)=-f(-x)=-log3(-x);
所以f(x)=
|
(2)由题意:当x>0时有log3x≤2,解得0<x≤9;
当x=0时,f(0)=0显然满足题意;
当x<0时有-log3(-x)≤2,即log3(-x)≥-2,解得x≤-
| 1 |
| 9 |
综上可得原不等式的解集为[0,9]∪(-∞,-
| 1 |
| 9 |
点评:本题考查了利用函数的奇偶性求函数解析式的方法,以及分段函数“分段处理”的解决问题的原则.属于基础题,难度不大.

练习册系列答案
 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案
相关题目
已知函数f(x)=m•9x-3x,若存在非零实数x0,使得f(-x0)=f(x0)成立,则实数m的取值范围是( )
A、m≥
| ||
B、0<m<
| ||
| C、0<m<2 | ||
| D、m≥2 |
下列函数在[
,π]上是增函数的是( )
| π |
| 2 |
| A、y=sinx |
| B、y=cosx |
| C、y=cos2x |
| D、y=sin2x |
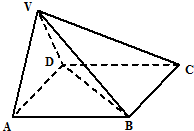 在四棱锥V-ABCD中,底面ABCD是正方形,侧面VAD是正三角形,平面VAD⊥底面ABCD.
在四棱锥V-ABCD中,底面ABCD是正方形,侧面VAD是正三角形,平面VAD⊥底面ABCD.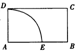 如图,四边形ABCD为矩形,AB=
如图,四边形ABCD为矩形,AB=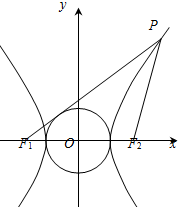 已知双曲线
已知双曲线