题目内容
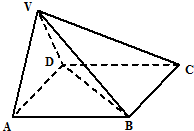 在四棱锥V-ABCD中,底面ABCD是正方形,侧面VAD是正三角形,平面VAD⊥底面ABCD.
在四棱锥V-ABCD中,底面ABCD是正方形,侧面VAD是正三角形,平面VAD⊥底面ABCD.(Ⅰ) 证明:AB⊥平面VAD;
(Ⅱ)求二面角A-VD-B的余弦值.
考点:二面角的平面角及求法,直线与平面垂直的判定
专题:空间位置关系与距离,空间角
分析:(Ⅰ)由平面VAD⊥平面ABCD,平面VAD∩平面ABCD=AD,又AB在平面ABCD内,AD⊥AB,即可证明AB⊥平面VAD.
(Ⅱ)由(Ⅰ)知AD⊥AB,AB⊥AV.依题意设AB=AD=AV=1,可求BV=BD=
.设VD的中点为E,连结AE、BE,则AE⊥VD,BE⊥VD,可得∠AEB是面VDA与面VDB所成二面角的平面角.又AE=
,BE=
,从而可求cos∠AEB的值.
(Ⅱ)由(Ⅰ)知AD⊥AB,AB⊥AV.依题意设AB=AD=AV=1,可求BV=BD=
| 2 |
| ||
| 2 |
| ||
| 2 |
解答:
 解:(Ⅰ)因为平面VAD⊥平面ABCD,平面VAD∩平面ABCD=AD,
解:(Ⅰ)因为平面VAD⊥平面ABCD,平面VAD∩平面ABCD=AD,
又AB在平面ABCD内,AD⊥AB,
所以AB⊥平面VAD.…(3分)
(Ⅱ)由(Ⅰ)知AD⊥AB,AB⊥AV.依题意设AB=AD=AV=1,
所以BV=BD=
.…(6分)
设VD的中点为E,连结AE、BE,则AE⊥VD,BE⊥VD,
所以∠AEB是面VDA与面VDB所成二面角的平面角.…(9分)
又AE=
,BE=
,
所以cos∠AEB=
=
.…(12分)
 解:(Ⅰ)因为平面VAD⊥平面ABCD,平面VAD∩平面ABCD=AD,
解:(Ⅰ)因为平面VAD⊥平面ABCD,平面VAD∩平面ABCD=AD,又AB在平面ABCD内,AD⊥AB,
所以AB⊥平面VAD.…(3分)
(Ⅱ)由(Ⅰ)知AD⊥AB,AB⊥AV.依题意设AB=AD=AV=1,
所以BV=BD=
| 2 |
设VD的中点为E,连结AE、BE,则AE⊥VD,BE⊥VD,
所以∠AEB是面VDA与面VDB所成二面角的平面角.…(9分)
又AE=
| ||
| 2 |
| ||
| 2 |
所以cos∠AEB=
| ||||||||
2×
|
| ||
| 7 |
点评:本题主要考查了直线与平面垂直的判定,二面角的余弦值的求法,正确作出并证明二面角的平面角是解题的关键,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 一几何体的三视图如图所示,若主视图和左视图都是等腰直角三角形,直角边长为1,则该几何体外接球的表面积为( )
一几何体的三视图如图所示,若主视图和左视图都是等腰直角三角形,直角边长为1,则该几何体外接球的表面积为( )| A、4π | B、3π | C、2π | D、π |