题目内容
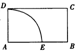 如图,四边形ABCD为矩形,AB=
如图,四边形ABCD为矩形,AB=| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:几何概型
专题:概率与统计
分析:由题意知本题是一个几何概型,由题意,试验包含的所有事件是∠BAD,而满足条件的事件是直线AP在∠CAB内时AP与BC相交时,即直线AP与线段BC有公共点,根据几何概型公式得到结果.
解答:
解:由题意知本题是一个几何概型,
试验包含的所有事件是∠BAD,
如图,连接AC交弧DE于P,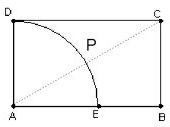
则tan∠CAB=
,
∴∠CAB=30°,
满足条件的事件是直线AP在∠CAB内时AP与BC相交时,即直线AP与线段BC有公共点
∴概率P=
=
=
,
故选:C.
试验包含的所有事件是∠BAD,
如图,连接AC交弧DE于P,

则tan∠CAB=
| 1 | ||
|
∴∠CAB=30°,
满足条件的事件是直线AP在∠CAB内时AP与BC相交时,即直线AP与线段BC有公共点
∴概率P=
| ∠CAB |
| ∠DAB |
| 30° |
| 90° |
| 1 |
| 3 |
故选:C.
点评:本题考查了几何摡型知识,几何概型的概率的值是通过长度、面积、和体积的比值得到.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
下列函数在其定义域内,既是奇函数又是单调递增函数的是( )
| A、y=sinx | ||
B、y=log
| ||
| C、y=x+8 | ||
| D、y=x3 |
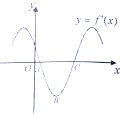 函数f(x)=sin(ωx+φ)的导函数y=f′(x)的部分图象如图所示,A,C为图象与x轴的两个交点,B为图象的最低点,若在曲线
函数f(x)=sin(ωx+φ)的导函数y=f′(x)的部分图象如图所示,A,C为图象与x轴的两个交点,B为图象的最低点,若在曲线