题目内容
已知函数y=f(2-x)的定义域为(2,6),求函数y=f(x-1)的定义域.
考点:函数的定义域及其求法
专题:函数的性质及应用
分析:由函数y=f(2-x)的定义域求出函数f(x)的定义域,从而求出函数y=f(x-1)的定义域.
解答:
解:∵函数y=f(2-x)的定义域为(2,6),
∴2<x<6,
即-6<-x<-2,
∴-4<2-x<0;
∴函数f(x-1)应满足
-4<x-1<0,
∴-3<x<1;
∴函数y=f(x-1)的定义域为(-3,1).
∴2<x<6,
即-6<-x<-2,
∴-4<2-x<0;
∴函数f(x-1)应满足
-4<x-1<0,
∴-3<x<1;
∴函数y=f(x-1)的定义域为(-3,1).
点评:本题考查了求函数定义域的问题,解题时要弄清函数y=f(2-x)、函数y=f(x)与y=f(x-1)的定义域的关系,是基础题.

练习册系列答案
相关题目
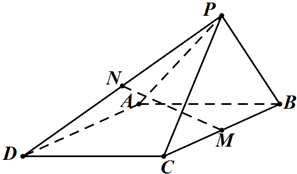 如图所示,在四棱锥P-ABCD中,四边形ABCD为菱形,∠ABC=60°,△PCB为正三角形,M,N分别为BC,PD的中点.
如图所示,在四棱锥P-ABCD中,四边形ABCD为菱形,∠ABC=60°,△PCB为正三角形,M,N分别为BC,PD的中点.